Question

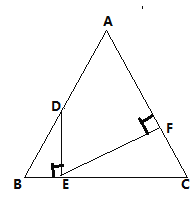
【题目】如图，等边△ABC的边长为12， D为AB边上一动点，过点D作DE⊥BC于点E．过点E作EF⊥AC于点F．
(1)若AD=2，求AF的长；
(2)当AD取何值时，DE=EF?

Answer 1

【答案】（1）；（2）当AD=4时，DE=EF．

【解析】

（1）根据已知条件得出△BDE和△CEF都是含30°的直角三角形，再根据含30°的直角三角形性质计算即可；

（2）当DE=EF时，可得出，进而根据BD=CE列出关于AD的等式，解出即可．

解：∵等边△ABC的边长为12，

∴∠B=∠C=60°，AB=BC=AC=12，

又∵DE⊥BC，EF⊥AC，

∴∠BED=∠CFE=90°，

∴∠BDE=∠CEF=30°，

若AD=2，

则BD=12-2=10，

∴在Rt△BDE中，，

∴CE=BC-BE=12-5=7，

∴在Rt△CEF中，，

∴

故．

（2）当DE=EF时，

在△BDE和△CEF中

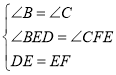
∴（AAS）

∴BD=CE

设AD=x

则，

∴，

∴

∴

解得：

∴当AD=4时，DE=EF．