题目内容
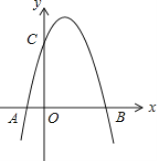
【题目】如图,二次函数![]() 的图象与x轴的一个交点为
的图象与x轴的一个交点为![]() ,另一个交点为A,且与y轴相交于C点
,另一个交点为A,且与y轴相交于C点
(1)求m的值及C点坐标;
(2)在直线BC上方的抛物线上是否存在一点M,使得它与B,C两点构成的三角形面积最大,若存在,求出此时M点坐标;若不存在,请简要说明理由
(3)P为抛物线上一点,它关于直线BC的对称点为Q,当四边形PBQC为菱形时,求点P的坐标(直接写出答案);
【答案】(1)![]()
![]()
(2) 存在, ![]()
(3)![]() 点坐标为(
点坐标为(![]() )或(
)或(![]() )
)
【解析】
![]() 将点
将点![]() 坐标代入得到
坐标代入得到![]() 的值,再令
的值,再令![]() 得到
得到![]() 点坐标;
点坐标;
![]() 点在直线
点在直线![]() 上方的抛物线上,要使
上方的抛物线上,要使![]() 面积最大,则
面积最大,则![]() 点的位置应在抛物线上且离直线的距离最远处,把直线
点的位置应在抛物线上且离直线的距离最远处,把直线![]() 向上平移和抛物线只有一个公共点时,此时的交点即为
向上平移和抛物线只有一个公共点时,此时的交点即为![]() 点的位置,然后根据二次函数的性质,求出
点的位置,然后根据二次函数的性质,求出![]() 值和
值和![]() 点坐标.
点坐标.
![]() 连接
连接![]() 交
交![]() 于点
于点![]() ,根据菱形的性质得到几何关系,用中点坐标公式和系数与直线位置的特殊关系,确定
,根据菱形的性质得到几何关系,用中点坐标公式和系数与直线位置的特殊关系,确定![]() 点坐标并求出直线
点坐标并求出直线![]() 的解析式,联立直线
的解析式,联立直线![]() 的解析式与抛物线解析式,即可求出
的解析式与抛物线解析式,即可求出![]() 点坐标.
点坐标.
解:![]() 将点
将点![]() 的坐标代入二次函数
的坐标代入二次函数![]() ,即
,即![]() ,解得
,解得![]() ,故二次函数解析式为
,故二次函数解析式为![]() ,令
,令![]() ,解得
,解得![]() ,故
,故![]() 点坐标为
点坐标为![]() ;
;
(2)存在,
理由:![]() ,
,![]()
![]() 直线
直线![]() 的解析式为
的解析式为![]() ,
,
当直线![]() 向上平移
向上平移![]() 单位后和抛物线只有一个公共点时,
单位后和抛物线只有一个公共点时,![]() 面积最大,
面积最大,
![]()
整理得:![]()
![]() ,
,
![]()
![]()
![]()
![]()
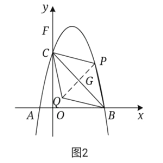
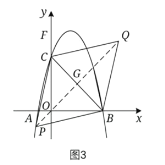
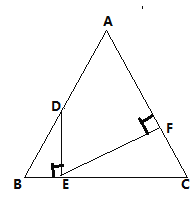
如图2、图3所示,连接![]() 交
交![]() 于点
于点![]() 。
。
因为四边形![]() 是菱形,所以
是菱形,所以![]() 为
为![]() 的中点,
的中点,
因为点![]() 的坐标分别为
的坐标分别为![]() 、
、![]() ,所以由中点坐标公式得
,所以由中点坐标公式得![]() 点坐标为
点坐标为![]() ,
,
由(2)可知直线![]() 的解析式为
的解析式为![]() ,
,
由于![]() ,所以设直线
,所以设直线![]() 的解析式为
的解析式为![]() ,
,
将![]() 代入,求得直线
代入,求得直线![]() 的解析式为
的解析式为![]() ,
,
将直线![]() 的解析式与抛物线解析式联立得:
的解析式与抛物线解析式联立得:
![]() ,消去
,消去![]() 得:
得:![]() ,
,
解得:![]() ,
,
将![]() 代入直线
代入直线![]() 的解析式得
的解析式得![]() ,
,
将![]() 代入直线
代入直线![]() 的解析式得
的解析式得![]() ,
,
故当四边形![]() 为菱形时,
为菱形时,![]() 点坐标为(
点坐标为(![]() )或(
)或(![]() ).
).

练习册系列答案
相关题目