题目内容
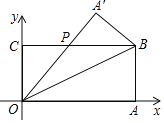
【题目】如图，平面直角坐标系中，长方形OABC，点A，C分别在x轴，y轴的正半轴上，点B（6，3），现将△OAB沿OB翻折至△OA′B位置，OA′交BC于点P．则点P的坐标为（ ）
A.（
，3）B.（
，3）C.（
，3）D.（
）
【答案】A
【解析】
由折叠的性质和矩形的性质证出OP=BP，设OP=BP=x，则PC=6﹣x，再用勾股定理建立方程9+（6﹣x）2=x2，求出x即可．
∵将△OAB沿OB翻折至△OA′B位置，OA′交BC于点P，
∴∠A'OB=∠AOB，
∵四边形OABC是矩形，
∴BC∥OA，
∴∠OBC=∠AOB，
∴∠OBC=∠A'OB，
∴OP=BP，
∵点B的坐标为（6，3），
∴AB=OC=3，OA=BC=6，
设OP=BP=x，则PC=6﹣x，
在Rt△OCP中，根据勾股定理得，OC2+PC2=OP2，
∴32+（6﹣x）2=x2，
解得：x=
，
∴PC=6﹣=
，
∴P（，3），
故选：A．
练习册系列答案
相关题目
