Question

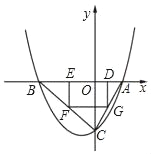
【题目】如图，抛物线y=ax2+bx﹣4（a≠0）与x轴交于A（2，0）、B（﹣4，0）两点，与y轴交于点C，矩形DEFG的一条边DE在线段AB上，顶点F，G分别在线段BC、AC上．

（I）求抛物线的解析式；

（II）若点D的坐标为（m，0），矩形DEFG的面积为S，求S与m的函数关系式，并指出m的取值范围；

（III）当矩形DEFG的面积S取最大值时，连接DF并延长至点M，使FM=kDF．若点M在抛物线上，求k的值．

Answer 1

【答案】（I）y=x2+x﹣4；（II）S矩形DEFG=12m﹣6m2（0＜m＜2）；（III）点M在抛物线上，此时k的值是：k=．

【解析】

(I)用待定系数法，将A、B的坐标代入y=ax2+bx﹣4，即可得到抛物线的解析式；

(II)表示出矩形的长和宽是解题的关键，由△ADG∽△AOC，从而=，得到DG=4-2m，由△BEF∽△BOC，从而=，得到DE=3m，因而得到S与m的函数关系式；

(III)当矩形的面积s取最大值时，就是函数的值是最大值时，根据二次函数的性质就可以求出相应的m的值，则矩形的四个顶点的坐标就可以求出，利用待定系数法就可以求出直线DF的解析式，便可求出直线DF与抛物线的交点M坐标，过M作x轴的垂线交x轴于H，有△OEF∽△OHM，则根据FM=kDF，即k==，便可求出k的值.

（I）∵抛物线y=ax2+bx﹣4（a≠0）与x轴交于A（2，0）、B（﹣4，0）两点，

∴，

解得：，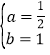

故抛物线解析式为：y=x2+x﹣4；

（II）由题意，=，而AO=2，OC=4，AD=2﹣m，

故DG=4﹣2m，

又=，EF=DG，得BE=4﹣2m，

∴DE=3m，

∴S矩形DEFG=DGDE=（4﹣2m）3m=12m﹣6m2（0＜m＜2）．

（III）∵S矩形DEFG=12m﹣6m2（0＜m＜2），

∴m=1时，矩形的面积最大，且最大面积是6．

当矩形面积最大时，其顶点为D（1，0），G（1，﹣2），F（﹣2，﹣2），E（﹣2，0），

设直线DF的解析式为y=kx+b，

则，

解得；，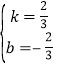

∴y=x﹣，

又抛物线P的解析式为：y=x2+x﹣4，

令x﹣=x2+x﹣4，可求出x=

设射线DF与抛物线P相交于点M，则M的横坐标为，

过M作x轴的垂线交x轴于H，

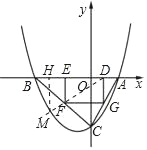
有k====，

点M在抛物线上，此时k的值是：k=．

故答案为：（I）y=x2+x﹣4；（II）S矩形DEFG=12m﹣6m2（0＜m＜2）；（III）点M在抛物线上，此时k的值是：k=．