题目内容
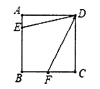
【题目】如图,正方形![]() 的边长为
的边长为![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,若
上,若![]() 是
是![]() 的中点,且
的中点,且![]() ,则
,则![]() 的长为_______.
的长为_______.
【答案】4
【解析】
延长F至G,使CG=AE,连接DG,由SAS证明△ADE≌△CDG,得出DE=DG,∠ADE=∠CDG,再证明△EDF≌△GDF,得出EF=GF,设AE=CG=x,则EF=GF=3+x,在Rt△BEF中,由勾股定理得出方程,解方程得出AE=2,从而求得BE的长即可.
解:延长F至G,使CG=AE,连接DG、EF,如图所示:
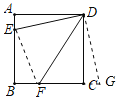
∵四边形ABCD是正方形,
∴AD=AB=BC=CD=6,∠A=∠B=∠DCF=∠ADC=90°,
∴∠DCG=90°,
在△ADE和△CDG中,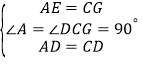 ,
,
∴△ADE≌△CDG(SAS),
∴DE=DG,∠ADE=∠CDG,
∴∠EDG=∠CDE+∠CDG=∠CDE+∠ADE=90°,
∵∠EDF=45°,
∴∠GDF=45°,
在△EDF和△GDF中,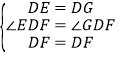 ,
,
∴△EDF≌△GDF(SAS),
∴EF=GF,
∵F是BC的中点,
∴BF=CF=3,
设AE=CG=x,则EF=GF=CF+CG=3+x,
在Rt△BEF中,由勾股定理得:![]() ,
,
解得:x=2,即AE=2,
∴BE=AB-AE=6-2=4.

 开心蛙口算题卡系列答案
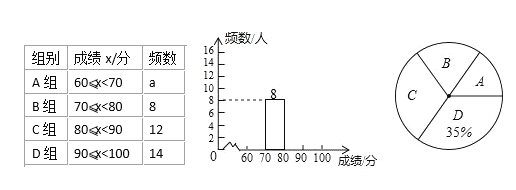
开心蛙口算题卡系列答案【题目】为声援扬州“运河申遗”,某校举办了一次运河知识竞赛,满分10分,学生得分为整数,成绩达到6分以上(包括6分)为合格,达到9分以上(包含9分)为优秀.这次竞赛中甲乙两组学生成绩分布的条形统计图如图所示.

(1)补充完成下面的成绩统计分析表:
组别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
甲组 | 6.7 | 3.41 | 90% | 20% | |
乙组 | 7.5 | 1.69 | 80% | 10% |
(2)小明同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上表可知,小明是 组的学生;(填“甲”或“乙”)
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你给出两条支持乙组同学观点的理由.
【题目】我市晶泰星公司安排![]() 名工人生产甲、乙两种产品,每人每天生产
名工人生产甲、乙两种产品,每人每天生产![]() 件甲产品或
件甲产品或![]() 件乙产品.根据市场行情测得,甲产品每件可获利
件乙产品.根据市场行情测得,甲产品每件可获利![]() 元,乙产品每件可获利
元,乙产品每件可获利![]() 元.而实际生产中,生产乙产品需要数外支出一定的费用,经过核算,每生产
元.而实际生产中,生产乙产品需要数外支出一定的费用,经过核算,每生产![]() 件乙产品,当天每件乙产品平均荻利减少
件乙产品,当天每件乙产品平均荻利减少![]() 元,设每天安排
元,设每天安排![]() 人生产乙产品.
人生产乙产品.
(1)根据信息填表:
产品种类 | 每天工人数(人) | 每天产量(件) | 每件产品可获利润(元) |
甲 |
| ||
乙 |
|
|
(2)若每天生产甲产品可获得的利润比生产乙产品可获得的利润多![]() 元,试问:该企业每天生产甲、乙产品可获得总利润是多少元?
元,试问:该企业每天生产甲、乙产品可获得总利润是多少元?