题目内容
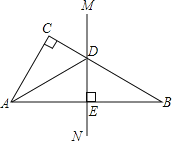
【题目】如图,已知函数![]() (x>0)的图象经过点A,B,点A的坐标为(1,2).过点A作AC∥y轴,AC=1(点C位于点A的下方),过点C作CD∥x轴,与函数的图象交于点D,过点B作BE⊥CD,垂足E在线段CD上,连接OC,OD.
(x>0)的图象经过点A,B,点A的坐标为(1,2).过点A作AC∥y轴,AC=1(点C位于点A的下方),过点C作CD∥x轴,与函数的图象交于点D,过点B作BE⊥CD,垂足E在线段CD上,连接OC,OD.
(1)求△OCD的面积;
(2)当BE=![]() AC时,求CE的长.
AC时,求CE的长.

【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)根据函数![]() (x>0)的图象经过点A(1,2),求函数解析式,再有AC∥y轴,AC=1求出C点坐标,然后根据CD∥x轴,求D点坐标,从而可求CD长,最后利用三角形面积公式求出△OCD的面积.
(x>0)的图象经过点A(1,2),求函数解析式,再有AC∥y轴,AC=1求出C点坐标,然后根据CD∥x轴,求D点坐标,从而可求CD长,最后利用三角形面积公式求出△OCD的面积.
(2)通过BE=![]() AC,求得B点坐标,进而求得CE长.
AC,求得B点坐标,进而求得CE长.
试题解析:解:(1)∵函数![]() (x>0)的图象经过点A(1,2),
(x>0)的图象经过点A(1,2),
∴![]() ,即k=2.
,即k=2.
∵AC∥y轴,AC=1,∴点C的坐标为(1,1).
∵ CD∥x轴,点D在函数图像上,∴点D的坐标为(2,1).
∴![]() .
.
(2)∵BE=![]() AC,∴BE=
AC,∴BE=![]() .
.
∵BE⊥CD,∴点B的纵坐标是![]() .∴点B的横坐标是
.∴点B的横坐标是![]() .
.
∴CE=![]() .
.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目