题目内容
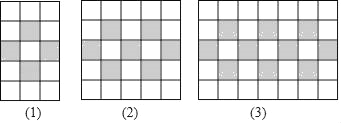
【题目】如图，图案由边长相等的黑、白两色正方形按一定规律拼接而成，第n个图案中白色正方形的个数比黑色正方形的个数多_____．（用含有n的代数式表示）
【答案】3+4n．
【解析】
通过观察图形很容易可知黑色正方形个数与图形的序号是相同的，即第n个图中黑色正方形的个数是3n+1；而白色正方形的个数是所有正方形的个数总和减去黑色正方形的个数即7n+4．所以白色正方形的个数-黑色正方形的个数（7n+4）-（3n+1）=3+4n．
由图可知
第1个图中：黑色正方形的个数是：4+3×0；白色正方形的个数是：11+7×0；
第2个图中：黑色正方形的个数是：4+3×1；白色正方形的个数是：11+7×1；
第3个图中：黑色正方形的个数是：4+3×2；白色正方形的个数是：11+7×2；
…
第n个图中：黑色正方形的个数是：4+3（n-1）=3n+1；白色正方形的个数是：11+7×（n-1）=7n+4；
所以第n个图案中白色正方形的个数比黑色的正方形个数多（7n+4）-（3n+1）=3+4n．
故答案为：3+4n．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
【题目】某校初一年级两个班的学生要到航天科普教育基地进行社会大课堂活动，两班学生共104人，其中初一（1）班有40多人，不足50人，教育基地门票价格如下：
购票张数 | 1～50张 | 51～100张 | 100张以上 |
每张票的价格 | 12元 | 10元 | 8元 |
原计划两班都以班为单位购票，则一共应付1240元，请回答下列问题：
（1）初一（1）班有多少人？
（2）你作为组织者如何购票最省钱？比原计划省多少钱？
【题目】某汽车行驶时油箱中余油量Q（L）与行驶时间t（h）的关系如表：
行驶时间t/h | 余油量Q/L |
1 | 42 |
2 | 34 |
3 | 26 |
4 | 18 |
5 | 10 |
（1）汽车行驶之前油箱中有汽油多少升？
（2）用行驶时间t的代数式表示余油量Q（直接写出答案）；
（3）当t＝
时，求余油量Q的值．
