题目内容
【题目】如图,CF是∠ACB的平分线,CG是∠ACB外角的平分线,FG∥BC交CG于点G,已知∠A=45°,∠B=55°,求∠FGC和∠FCG的度数. 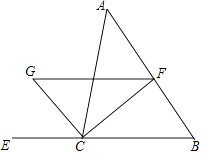
【答案】解:∵∠ACE=∠A+∠B=45°+55°=100°, 又∵CG是∠ACE的平分线,
∴∠GCE=∠ACG= ![]() ∠ACE=50°,
∠ACE=50°,
∵FG∥BC,
∴∠FGC=∠GCE=50°.
∵CF平分∠ACB,
∴∠ACF= ![]() ∠ACB,
∠ACB,
又∵∠ACG= ![]() ∠ACE,
∠ACE,
∴∠FCG=∠ACF+∠ACG= ![]() ∠ACB+
∠ACB+ ![]() ∠ACE=
∠ACE= ![]() ×180°=90°.
×180°=90°.
【解析】首先利用三角形的外角等于不相邻的两个内角的和求得∠ACE的度数,然后根据角的平分线的定义求得∠GCE的度数,再利用平行线的性质求得∠FGC;利用角的平分线的定义可以得到∠FCG=∠ACF+∠ACG= ![]() (∠ACB+∠ACE),从而求得∠FCG.
(∠ACB+∠ACE),从而求得∠FCG.
【考点精析】掌握平行线的性质是解答本题的根本,需要知道两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.

练习册系列答案
相关题目