题目内容
【题目】爸爸为了检查小明对平行线的条件与性质这部分知识的掌握情况,给他出了一道题:如图,AB∥DE,∠B=80°,CM平分∠BCD,CN⊥CM,求∠NCE的度数.小明稍加思索,就做出来了,你知道他是怎样解的吗?请把你的推理过程写下来吧. 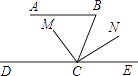
【答案】解:∵AB∥DE,∠B=80° ∴∠B+∠DCB=180°,
∴∠DCB=180°﹣80°=100°,
∵CM平分∠BCD,
∴∠DCM= ![]() ∠BCD=
∠BCD= ![]() ×100°=50°,
×100°=50°,
∵CM⊥CN,
∴∠MCN=90°,
∴∠ECN=180°﹣90°﹣50°=40°.
【解析】先根据AB∥DE,得出∠B+∠DCB=180°,故可得出∠DCB的度数,再根据CM平分∠BCD,可知∠DCM= ![]() ∠BCD,由CM⊥CN,可知∠MCN=90°,根据∠ECN=180°﹣∠MCN﹣∠DCM即可得出结论.
∠BCD,由CM⊥CN,可知∠MCN=90°,根据∠ECN=180°﹣∠MCN﹣∠DCM即可得出结论.
【考点精析】掌握垂线的性质和平行线的性质是解答本题的根本,需要知道垂线的性质:1、过一点有且只有一条直线与己知直线垂直.2、垂线段最短;两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.

练习册系列答案
相关题目