题目内容
【题目】如图,AD⊥BC,D为垂足,DE∥AB,∠1=∠2,图中EF与BC垂直吗?为什么? 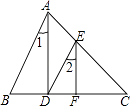
【答案】解:垂直 理由:∵DE∥AB,
∴∠1=∠ADE,
∵∠1=∠2,
∴∠2=∠ADE,
∴AD∥EF,
∴∠ADB=∠EFB,
∵AD⊥BC,
∴∠ADB=90°,
∴∠EFB=90°,
∴EF⊥BC
【解析】先根据DE∥AB,∠1=∠2,可得∠2=∠ADE,即可得出AD∥EF,进而得到∠ADB=∠EFB=90°,进而得出EF⊥BC.
【考点精析】掌握垂线的性质和平行线的性质是解答本题的根本,需要知道垂线的性质:1、过一点有且只有一条直线与己知直线垂直.2、垂线段最短;两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.

练习册系列答案
相关题目