Question

【题目】如图，点A．B．C分别是⊙O上的点，∠B=60°，AC=3，CD是⊙O的直径，P是CD延长线上的一点，且AP=AC．

（1）求证：AP是⊙O的切线；

（2）求PD的长．

Answer 1

【答案】（1）相切；（2）

【解析】试题分析：（1）连接OA，利用等腰三角形的性质和角的关系求出∠OAP=90°，得出OA⊥AP即可；（2）连接AD，△ACD中利用tan30°求出AD=,然后证明∠P=∠PAD得出PD=AD=．

试题解析：（1）连接OA．

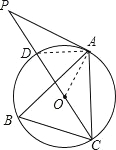
∵∠B=60°，

∴∠AOC=2∠B=120°，

又∵OA=OC，

∴∠ACP=∠CAO=30°，

∴∠AOP=60°，

∵AP=AC，

∴∠P=∠ACP=30°，

∴∠OAP=90°，

∴OA⊥AP，

∴AP是⊙O的切线，

（2）连接AD．

∵CD是⊙O的直径，

∴∠CAD=90°，

∴AD=AC×tan30°=3×=，

∵∠ADC=∠B=60°，

∴∠PAD=∠ADC﹣∠P=60°﹣30°，

∴∠P=∠PAD，

∴PD=AD=．