题目内容
【题目】如图,AB为⊙O的直径,C为⊙O上一点,作CD⊥AB,垂足为D,E为弧BC的中点,连接AE、BE,AE交CD于点F.
(1)求证:∠AEC=90°﹣2∠BAE;
(2)过点E作⊙O的切线,交DC的延长线于G,求证:EG=FG;
(3)在(2)的条件下,若BE=4![]() ,CF=6,求⊙O的半径.
,CF=6,求⊙O的半径.



【答案】(1)(2)证明见解析;(3)⊙O的半径为10.
【解析】
![]() 连接AC、BC,先根据等弧得:∠CAE=∠BAE,则∠CAB=2∠BAE,再由直径所对的圆周角为直角得:∠ACB=90°,直角三角形的两锐角互余得:
连接AC、BC,先根据等弧得:∠CAE=∠BAE,则∠CAB=2∠BAE,再由直径所对的圆周角为直角得:∠ACB=90°,直角三角形的两锐角互余得:
∠CAB+∠CBA=90°,等量代换可得结论;
(2)如图2,连接EO,设![]() 证明
证明![]() 则
则![]()
(3)如图3,作辅助线,构建直角三角形,证明![]() 则
则![]() ,由(2)得
,由(2)得![]() ,则CM∥EG,
,则CM∥EG,![]() 设
设![]() 则
则![]() 根据三角函数得:
根据三角函数得:![]() 列式求得x的值,在△OBM中,设
列式求得x的值,在△OBM中,设![]() 则
则![]() 根据勾股定理列方程可得结论.
根据勾股定理列方程可得结论.
证明:(1)如图1,连接AC、BC,
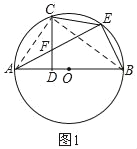
∴∠CEA=∠CBA,
∵E为![]() 的中点,
的中点,
∴![]() =
=![]() ,
,
∴∠CAE=∠BAE,
∴![]()
∵AB是直径,
∴∠ACB=90°,
∴∠CAB+∠CBA=90°,
∴2∠BAE+∠AEC=90°,
∴∠AEC=90°﹣2∠BAE;
(2)如图2,连接EO,
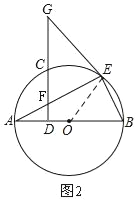
∵OA=OE,
∴∠OEA=∠OAE,
设∠OEA=∠OAE=α,
∵EG为切线,
∴OE⊥EG,
∴∠OEG=90°,
∴![]()
∵DG⊥AB,
∴∠FDA=90°,
∴∠FAD+∠AFD=90°,
∴![]()
∴![]()
∴GE=GF;
(3)如图3,连接CE、CB、OE、OC,CB与AE交于点N,CB与OE交于点M,
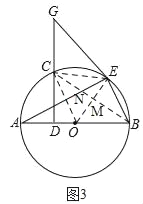
∵E为![]() 的中点,
的中点,
∴∠COM=∠BOM,
∵OC=OB,
∴OM⊥BC,
∴∠OMB=90°,
由(2)得∠GEM=90°,
∴CM∥EG,
∴∠GEF=∠CNF,
∵∠GFE=∠GEF,
∴∠CFE=∠CNF,
∴![]()
设![]() 则
则![]()
![]()
∴![]()
解得:![]() (舍),
(舍),
![]()
由勾股定理得:![]()
在△OBM中,设![]() 则
则![]()
![]()
即![]()
∴![]()
∴![]()
则⊙O的半径为10.







