题目内容
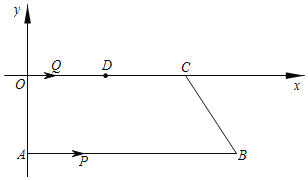
【题目】如图，边长为4的等边三角形AOB的顶点O在坐标原点，点A在x轴的正半轴上，点B在第一象限．点P从点O出发，沿x轴以每秒1个单位长的速度向点A匀速运动，当点P到达点A时停止运动，设点P运动的时间是t秒．将线段BP的中点绕点P按顺时针方向旋转60°得点C，点C随点P的运动而运动，连接CP、CA．过点P作PD⊥OB于D点
（1）直接写出BD的长并求出点C的坐标（用含t的代数式表示）
（2）在点P从O向A运动的过程中，△PCA能否成为直角三角形？若能，求t的值．若不能，请说明理由；
（3）点P从点O运动到点A时，点C运动路线的长是多少？
【答案】
（1）解：∵△AOB是等边三角形，
∴OB=OA=AB=4，∠BOA=∠OAB=∠ABO=60°．
∵PD⊥OB，
∴∠PDO=90°，
∴∠OPD=30°，
∴OD= 
OP．
∵OP=t，
∴OD= t，
∴BD=4﹣ t．
在Rt△OPD中，由勾股定理，得PD= 
t，
如图（1），过C作CE⊥OA于E，
则∠PEC=90°，
∵线段BP的中点绕点P按顺时针方向旋转60°得点C，
∴∠BPC=60°．
∵∠OPD=30°，
∴∠BPD+∠CPE=90°．
∴∠DBP=∠CPE
∴△PCE∽△BPD，
∴ 
= 
= 
，
∴ 
= = 
，
∴CE= 
，PE=2﹣ 
，
∴OE=OP+PE=2+ 
，
∴C（2+ ， ）
（2）解：如图（3），当∠PCA=90度时，作CF⊥PA，
∴△PCF∽△ACF，
∴ 
= 
，
∴CF2=PFAF，
∵PF=2﹣ 
t，AF=4﹣OF=2﹣ 
t，CF= 
t，
∴（ t）2=（2﹣ t）（2﹣ t），
解得t=2，
此时P是OA的中点．
如图（2），
当∠CAP=90°时，C的横坐标就是4，
∴2+ t=4，
解得t= 
（3）解：设C（x，y），
∴x=2+ t，y= t，
∴y= 
x﹣ 
，
∴C点的运动痕迹是一条线段（0≤t≤4）．
当t=0时，C1（2，0），
当t=4时，C2（5， 
），
∴由两点间的距离公式得：C1C2=2 ．
故点C运动路线的长为：2
【解析】（1）利用30度角的性质和旋转性质、相似三角形性质，即△PCE∽△BPD，对应边成比例可求出C坐标；（2）可先假设△PCA能成为直角三角形，分类讨论，当∠PCA=90度时或∠CAP=90°，可利用相似性质列出对应边成比例式子，进行求解;（3）可设出设C（x，y），构建参数方程x=2+ t，y= t，消去参数即可得到y= x﹣ .
