题目内容
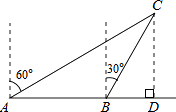
【题目】如图,一个长5m的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为4m,如果梯子的顶端A沿墙下滑1m至C点.
(1)求梯子底端B外移距离BD的长度;
(2)猜想CE与BE的大小关系,并证明你的结论.

【答案】(1)BD=1m;(2)CE与BE的大小关系是CE=BE,证明见解析.
【解析】
(1)利用勾股定理求出OB,求出OC,再根据勾股定理求出OD,即可求出答案;
(2)求出△AOB和△DOC全等,根据全等三角形的性质得出OC=OB,∠ABO=∠DCO,求出∠OCB=∠OBC,求出∠EBC=∠ECB,根据等腰三角形的判定得出即可.
(1)∵AO⊥OD,AO=4m,AB=5m,
∴OB=![]() =3m,
=3m,
∵梯子的顶端A沿墙下滑1m至C点,
∴OC=AO﹣AC=3m,
∵CD=AB=5m,
∴由勾股定理得:OD=4m,
∴BD=OD﹣OB=4m﹣3m=1m;
(2)CE与BE的大小关系是CE=BE,证明如下:
连接CB,由(1)知:AO=DO=4m,AB=CD=5m,
∵∠AOB=∠DOC=90°,
在Rt△AOB和Rt△DOC中
![]() ,
,
∴Rt△AOB≌Rt△DOC(HL),
∴∠ABO=∠DCO,OC=OB,
∴∠OCB=∠OBC,
∴∠ABO﹣∠OBC=∠DCO﹣∠OCB,
∴∠EBC=∠ECB,
∴CE=BE.

练习册系列答案
相关题目