题目内容
【题目】我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做“湘一四边形”.
(1)已知:如图1,四边形![]() 是“湘一四边形”,
是“湘一四边形”,![]() ,
,![]() ,
,![]() .则
.则![]() ,
, ![]() ,若
,若![]() ,
,![]() ,则
,则![]() (直接写答案)
(直接写答案)
(2)已知:在“湘一四边形”![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .求对角线
.求对角线![]() 的长(请画图求解),
的长(请画图求解),
(3)如图(2)所示,在四边形![]() 中,若
中,若![]() ,当
,当![]() 时,此时四边形
时,此时四边形![]() 是否是“湘一四边形”,若是,请说明理由:若不是,请进一步判断它的形状,并给出证明.
是否是“湘一四边形”,若是,请说明理由:若不是,请进一步判断它的形状,并给出证明.
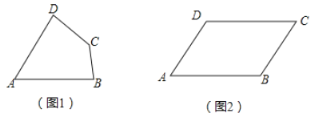
【答案】(1)85°,115°,3;(2)AC的长为![]() 或
或![]() ;(3)四边形ABCD不是“湘一四边形”,四边形ABCD是平行四边形,理由见解析
;(3)四边形ABCD不是“湘一四边形”,四边形ABCD是平行四边形,理由见解析
【解析】
(1)连接BD,根据“湘一四边形”的定义求出∠B,∠C,利用等腰三角形的判定和性质证明BC=DC即可.
(2)分两种情形:①如图1-1,∠B=∠D=90°时,延长AD,BC交于点E.②如图2-1中,∠A=∠C=60°时,过D分别作DE⊥AB于E,DF⊥BC于点F,分别求解即可解决问题.
(3)结论:四边形ABCD不是“湘一四边形”,四边形ABCD是平行四边形.如图2中,作CN⊥AD于N,AM⊥CB于M.利用全等三角形的性质证明AD=BC即可解决问题.
解:(1)如图1中,连接BD.
∵四边形ABCD是湘一四边形,∠A≠∠C,
∴∠B=∠D=85°,
∵∠A=75°,
∴∠C=360°-75°-2×85°=115°,
∵AD=AB,
∴∠ADB=∠ABD,
∵∠ADC=∠ABC,
∴∠CDB=∠CBD,
∴BC=CD=3,
故答案为85°,115°,3.
(2)①如图1-1,∠B=∠D=90°时,延长AD,BC交于点E,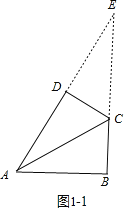
∵∠DAB=60°,
∴∠E=30°,
又∵AB=4,AD=3
∴BE=4![]() ,AE=8,DE=5,
,AE=8,DE=5,
∴CE=![]() ,
,
∴BC=BE-CE=4![]() ,
,
∴AC=![]() ,
,
②如图2-1中,∠A=∠C=60°时,过D分别作DE⊥AB于E,DF⊥BC于点F,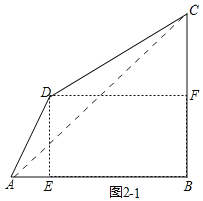
∵∠DAB=∠BCD=60°,
又∵AB=4,AD=3,
∴AE=![]() ,DE=BF=
,DE=BF=![]() ,
,
∴BE=DF=![]() ,
,
∴CF=DFtan30°=![]() ×
×![]() ,
,
∴BC=CF+BF=![]() ,
,
∴AC=![]() ,
,
综合以上可得AC的长为![]() 或
或![]() .
.
(3)结论:四边形ABCD不是“湘一四边形”,四边形ABCD是平行四边形.
理由:如图2中,作CN⊥AD于N,AM⊥CB于M.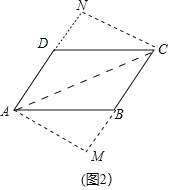
∵∠ADB=∠ABC,
∴∠CDN=∠ABM,
∵∠N=∠M=90°,CD=AB,
∴△CDN≌△ABM(AAS),
∴CN=AM,DN=BM,
∵AC=CA,CN=AM,
∴Rt△ACN≌Rt△CAM(HL),
∴AN=CM,∵DN=BM,
∴AD=BC,∵CD=AB,
∴四边形ABCD是平行四边形.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案