Question

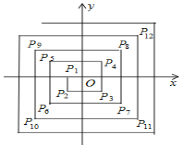
【题目】如图，在平面直角坐标系中，从点P1（﹣1，0），P2（﹣1，﹣1），P3（1，﹣1），P4（1，1），P5（﹣2，1），P6（﹣2，﹣2），…依次扩展下去，则P2020的坐标为_____．

Answer 1

【答案】（505，505）

【解析】

根据各个点的位置关系，可得出下标为4的倍数的点在第一象限，被4除余1的点在第二象限，被4除余2的点在第三象限，被4除余3的点在第四象限，点P2020在第一象限，且横、纵坐标=2020÷4，再根据第二项象限点的规律即可得出结论．

解：分析各点坐标可发现，下标为4的倍数的点在第一象限，被4除余1的点在第二象限，被4除余2的点在第三象限，被4除余3的点在第四象限，

∵，

∴点P2020在第一象限，

又∵第一象限的点P4（1，1），点P8（2，2），点P12（3，3），

可知，点P2020（505，505），

故答案为：（505，505）．