题目内容
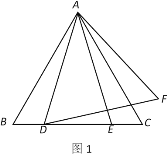
【题目】如图 1,已知线段 AB=12 cm,点 C 为线段 AB 上的一动点(点 C 不与 A,B 重合),点D,E 分别是 AC 和 BC 的中点.
(1)若点 C 恰好是 AB 的中点,则 DE= cm;
(2)若 AC=4 cm,求 DE的长;
(3)试说明当点C在线段 AB 上运动时,DE 的长不变;
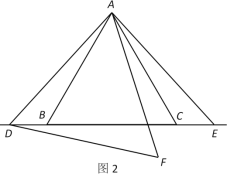
(4)如图 2,已知∠AOB=120°,在∠AOB 的内部任画一条射线 OC.
①请分别画出∠AOC 和∠COB 的平分线 OD,OE(不要求尺规作图);
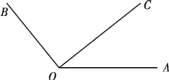
②说明∠DOE 的度数与射线 OC 的位置无关.
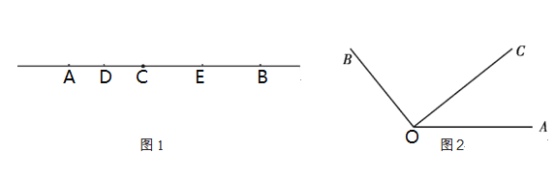
【答案】(1)6;(2)6cm;(3)证明见解析;(4)①答案见解析;②证明见解析.
【解析】
(1)根据中点的概念,通过线段的和差倍分进行计算即可得解;
(2)根据中点的概念,通过线段的和差倍分进行计算即可得解;
(3)根据中点的概念,通过线段的和差倍分进行计算即可得解;
(4)根据角平分线的概念,通过角的和差倍分进行计算即可得解.
(1)∵C是AB中点,AB=12cm,
∴![]() ,
,
∵点D,E分别是AC和BC的中点,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ;
;
(2)∵![]() ,
,![]() ,
,
∴![]() ,
,
∵点![]() ,
,![]() 分别是
分别是![]() 和
和![]() 的中点,
的中点,
∴![]() ,
,![]() ,
,
∴![]() ;
;
(3)∵点![]() ,
,![]() 分别是
分别是![]() 和
和![]() 的中点,
的中点,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴当点![]() 在线段
在线段![]() 上运动时,
上运动时,![]() 的长不变且为
的长不变且为![]() ;
;
(4)①如图,
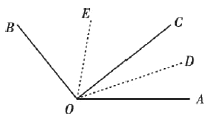
射线![]() 与
与![]() 为所求的角平分线.
为所求的角平分线.
②∵![]() 与
与![]() 分别平分
分别平分![]() 和
和![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() 的度数与射线
的度数与射线![]() 的位置无关.
的位置无关.

练习册系列答案
相关题目