题目内容
【题目】已知：如图，在平面直角坐标系中，O为坐标原点，四边形OABC是矩形，点A、C的坐标分别为A（7，0），C（0，4），点D的坐标为（5，0），点P在BC边上运动. 当△ODP是腰长为5的等腰三角形时，点P的坐标为______________.
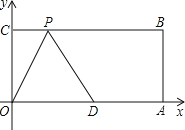
【答案】(2，4)或（3，4）
【解析】
当△ODP是腰长为5的等腰三角形时，考虑到BD<OD,所以有两种情况，OD=PD或OP=OD.再根据勾股定理即可求出点Ｐ到ｙ轴的距离，从而求出点Ｐ的坐标
解：∵A（7，0），C（0，4），
∴AB=OC=4 OA=7，
∵D的坐标为（5，0），
∴OD=5，
∴AD=2，
∵四边形OABC是矩形，
∴∠A=90°，
∴ＢＤ＝
＝２
＜５＝ＯＤ，
故有三种情况： OD=PD或OD=OP或者OP=PD，
①当OD=PD时，p（2，4）或P（8，4）（舍去）
②当OD=OP时，PC=
=
=3.
故此时点P的坐标为（3，4）.
③当OP=PD时，P(
,4)（舍去）.
故答案为：（2，4）或（3，4）．
练习册系列答案
相关题目
