题目内容
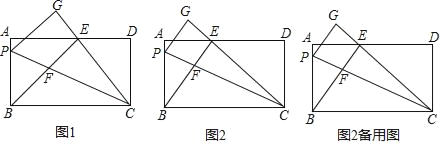
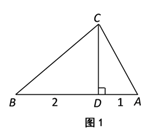
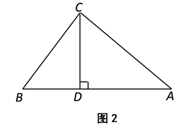
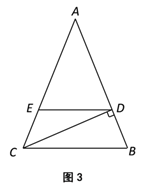
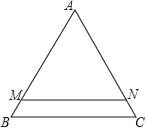
【题目】如图,△ABC中,AB=AC,∠A=60°,BC=6,直线MN∥BC,且分别交边AB,AC于点M,N,已知直线MN将△ABC分为△AMN和梯形MBCN面积之比为5:1的两部分,如果将线段AM绕着点A旋转,使点M落在边BC上的点D处,那么BD=_____.
【答案】3±![]()
【解析】过点A作AE⊥BC于点E,由AB=AC、∠A=60°,可得出△ABC为等边三角形,进而可得出BE、AE的长度,由MN∥BC可得出△AMN∽△ABC,根据相似三角形的性质结合直线MN将△ABC分为△AMN和梯形MBCN面积之比为5:1的两部分,可求出AM的长度,由旋转的性质可得出AD的长度.在Rt△ADE中,利用勾股定理可求出DE的长度,再根据BD=BE±DE,即可求出BD的长度.
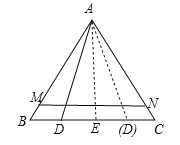
过点A作AE⊥BC于点E,如图所示.
∵AB=AC,∠A=60°,∴△ABC为等边三角形,∴BE=CE=![]() BC=3,AE=
BC=3,AE=![]() BC=3
BC=3![]() .
.
∵MN∥BC,∴△AMN∽△ABC,∴![]() =(
=(![]() )2.
)2.
∵直线MN将△ABC分为△AMN和梯形MBCN面积之比为5:1的两部分,∴![]() =(
=(![]() )2=
)2=![]() ,即(
,即(![]() )2=
)2=![]() ,解得:AM=
,解得:AM=![]() ,∴AD=AM=
,∴AD=AM=![]() .
.
在Rt△ADE中,∠AED=90°,AD=![]() ,AE=3
,AE=3![]() ,∴DE=
,∴DE=![]() ,∴BD=BE±DE=3±
,∴BD=BE±DE=3±![]() .
.
故答案为:3±![]() .
.

【题目】某市为了鼓励居民节约用水,采用分阶段计费的方法按月计算每户家庭的水费:月用水量不超过20m3时,按2元/m3计算;月用水量超过20m3时,其中的20m3仍按2元/m3计算,超过部分按2.6元/m3计算.设某户家庭月用水量xm3.
月份 | 4月 | 5月 | 6月 |
用水量 | 15 | 17 | 21 |
(1)用含x的式子表示:
当0≤x≤20时,水费为 元;
当x>20时,水费为 元.
(2)小花家第二季度用水情况如上表,小花家这个季度共缴纳水费多少元?
【题目】电影《我和我的祖国》讲述了新中国成立70年间普通百姓与共和国息息相关的故事.影片上映15天就斩获票房26亿元人民币,口碑票房实现双丰收.据统计,10月8日,该电影在重庆的票房收入为140万元,接下来7天的票房变化情况如下表(正数表示比前一天增加的票房,负数表示比前一天减少的票房):
日期 | 9日 | 10日 | 11日 | 12日 | 13日 | 14日 | 15日 |
票房变化(万元) |
|
| 0 |
|
|
|
|
(1)这7天中,票房收入最多的是10月________日,票房收入最少的是10月________日;
(2)根据上述数据可知,这7天该电影在重庆的平均票房收入为多少万元?