Question

【题目】在矩形ABCD中，已知AD=4，AB=3，点P是直线AD上的一点，PE⊥AC，PF⊥BD，E，F分别是垂足，AG⊥BD与点G，

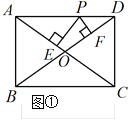
(1) 如图①点P在线段AD上，求PE+PF的值；

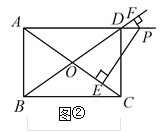
(2) 如图②点P在直线AD上，求PEPF的值.

Answer 1

【答案】（1）；（2）.

【解析】

（1）过点A作AG⊥BD于点G，连接PO，首先利用勾股定理求出BD=5，然后利用三角形面积列式求出AG，根据S△AOD=S△AOP+S△POD可得OD·AG=OA·PE +OD·PF，结合OA=OD可求出AG=PE+PF=；

（2）根据S△AOD=S△AOPS△POD可得OD·AG=OA·PEOD·PF，结合OA=OD可求出AG=PEPF=.

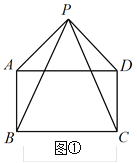
解：(1)如图③，过点A作AG⊥BD于点G，连接PO，

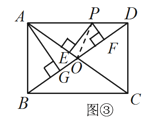
∵四边形ABCD是矩形，

∴OA＝OD，∠BAD＝90°.

在Rt△ABD中，AD=4，AB=3，

由勾股定理得BD=.

∵AG⊥BD，

∴S△ABD=AB·AD=BD·AG

∴AB·AD=BD·AG

∴3×4=5AG，解得AG=.

∵S△AOD=S△AOP+S△POD，

∴OD·AG=OA·PE +OD·PF.

∵OA=OD，

∴AG=PE+PF.

∴PE+PF= AG=；

(2)如图④，过点A作AG⊥BD于点G，连接PO，

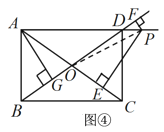
∵S△AOD=S△AOPS△POD，

∴OD·AG=OA·PEOD·PF，

∵OA=OD，

∴AG=PEPF，

∴PEPF= AG=.