题目内容
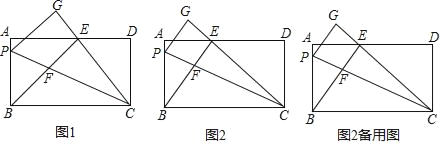
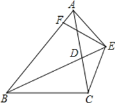
【题目】已知，△ABC为等边三角形，点D，E为直线BC上两动点，且BD＝CE． 点F，点E关于直线AC成轴对称，连接AE，顺次连接A，D，F．
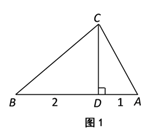
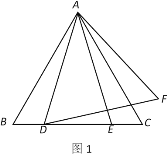
（1）如图1，若点D，点E在边BC上，试判断△ADF的形状并说明理由；
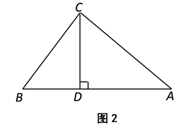
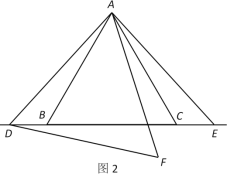
（2）如图2，若点D，点E在边BC外，求证：
．
【答案】（1）△ADF为等边三角形，见解析；（2）见解析
【解析】
（1）先根据等边三角形的性质得出
，然后证明
，得出
，再根据对称的性质得出
,从而有
，则结论可证；
（2）先根据等边三角形的性质得出，然后证明，得出，再根据对称的性质得出,从而有，则△ADF为等边三角形，则
，通过等量代换即可得出答案．
解：（1）△ADF为等边三角形，理由如下：
∵△ABC为等边三角形，
∴ ．
在
和
中，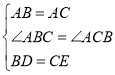
，
．
∵点F，点E关于直线AC成轴对称，
，
．
，
，
即 ,
∴△ADF为等边三角形．
（2）∵△ABC为等边三角形，
∴ ．
在和中，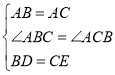
，
．
∵点F，点E关于直线AC成轴对称，
，
．
，
，
∴△ADF为等边三角形．
∵
∴
练习册系列答案
智慧小复习系列答案
相关题目
