��Ŀ����
����Ŀ����ͼ����֪������y=ax2+2x+c��y�ύ�ڵ�A��0��6������x�ύ�ڵ�B��6��0������P���߶�AB�Ϸ��������ϵ�һ�����㣮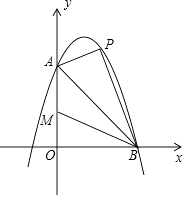
��1�������������ߵı���ʽ���䶥�����ꣻ
��2������P�ƶ��������ߵ�ʲôλ��ʱ��ʹ�á�PAB=75�㣬�����ʱ��P�����ꣻ
��3������P��A��������߶�AB�Ϸ������������յ�B�ƶ������ƶ��У���P�ĺ�������ÿ��1����λ���ȵ��ٶȱ䶯�����ͬʱ��M��ÿ��1����λ���ȵ��ٶ���AO���յ�O�ƶ�����P��M�ƶ��������յ�ʱֹͣ���������Ƶ��ƶ�t��ʱ�����ı���PAMB�����S����t�ĺ�������ʽ������tΪ��ֵʱ��S�����ֵ�����ֵ�Ƕ��٣�
���𰸡�
��1��
�⣺�������⣬��A��0��6����B��6��0�����������߽���ʽ�ɵ� ![]() �����
����� 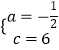 ��
��
�������ߵı���ʽΪy=�� ![]() x2+2x+6��
x2+2x+6��
��y=�� ![]() x2+2x+6=��
x2+2x+6=�� ![]() ��x��2��2+8��
��x��2��2+8��
�������ߵĶ�������Ϊ��2��8��
��2��
�⣺��ͼ1����P��PC��y���ڵ�C��
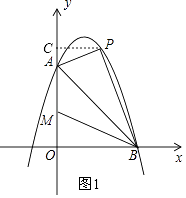
��OA=OB=6��
���OAB=45�㣬
�൱��PAB=75��ʱ����PAC=60�㣬
��tan��PAC= ![]() ����
���� ![]() =
= ![]() ��
��
��AC=m����PC= ![]() m��
m��
��P�� ![]() m��6+m����
m��6+m����
��P��������������߱���ʽ�ɵ�6+m=�� ![]() ��
�� ![]() m��2+2
m��2+2 ![]() m+6�����m=0��m=
m+6�����m=0��m= ![]() ��
�� ![]() ��
��
�����飬P��0��6�����A�غϣ��������⣬��ȥ��
�������P��������4�� ![]() ��
�� ![]() +
+ ![]() ��
��
��3��
�⣺������֧���ƶ�t��ʱ����P��t���� ![]() t2+2t+6����M��0��6��t����
t2+2t+6����M��0��6��t����
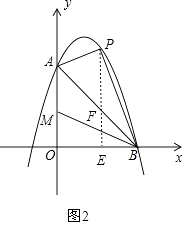
��ͼ2����PE��x���ڵ�E����AB�ڵ�F����EF=EB=6��t��
��F��t��6��t����
��FP= ![]() t2+2t+6����6��t��=��
t2+2t+6����6��t��=�� ![]() t2+3t��
t2+3t��
�ߵ�A��PE�ľ�����OE����B��PE�ľ������BE��
��S��PAB= ![]() FPOE+
FPOE+ ![]() FPBE=
FPBE= ![]() FP��OE+BE��=
FP��OE+BE��= ![]() FPOB=
FPOB= ![]() ������
������ ![]() t2+3t����6=��
t2+3t����6=�� ![]() t2+9t����S��AMB=
t2+9t����S��AMB= ![]() AMOB=
AMOB= ![]() ��t��6=3t��
��t��6=3t��
��S=S�ı���PAMB=S��PAB+S��AMB=�� ![]() t2+12t=��
t2+12t=�� ![]() ��t��4��2+24��
��t��4��2+24��
�൱t=4ʱ��S�����ֵ�����ֵΪ24
����������1����A��B���꣬���ô���ϵ��������������ߵı���ʽ����Ϊ����ʽ����ö������ꣻ��2����P��PC��y���ڵ�C������������á�PAC=60�㣬����AC=m����Rt��PAC�У��ɱ�ʾ��PC�ij����Ӷ�����m��ʾ��P�����꣬���������߽���ʽ�����m��ֵ���������P�����ꣻ��3����t�ɱ�ʾ��P��M�����꣬��P��PE��x���ڵ�E����AB�ڵ�F����ɱ�ʾ��F�����꣬�Ӷ�����t��ʾ��PF�ij����Ӷ��ɱ�ʾ����PAB�����������S�ı���PAMB=S��PAB+S��AMB �� �ɵõ�S����t�Ķ��κ��������ö��κ��������ʿ���������ֵ��

 �Ͻ�ƽ��У����ϵ�д�
�Ͻ�ƽ��У����ϵ�д�








