Question

【题目】如图，已知AO为Rt△ABC的角平分线，∠ACB＝90°，以O为圆心，OC为半径的圆分别交AO，BC于点D，E，连接ED并延长交AC于点F．

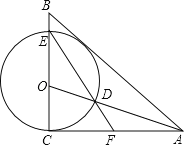
（1）求证：AB是⊙O的切线；

（2）当时，求的值；

（3）在（2）的条件下，若⊙O的半径为4，求的值．

Answer 1

【答案】（1）证明见解析；（2）；（3）的值为．

【解析】

（1）作OG⊥AB于点G，运用角平分线的性质证明；

（2）根据线段比例关系，设未知数表示线段AC、BC的长度，运用勾股定理和切线长定理，求出BG，易证△∽△，根据相似三角形对应线段成比例求出OG，进而分别求出CE

和BE，据此求解；

（3）由CE＝＝2×4，求出的值，从而求出AC、BC，运用勾股定理求出AO，则AD=AO-OD，证明△DFA∽△CDA，根据对应线段成比例求出AF，则CF=AC-AF，进而求出．

（1）证明：作OG⊥AB于点G．

∵∠ACB＝90°，

∴BC⊥AC，

∵AO为Rt△ABC的角平分线，

∴OG=OC

∴AB是⊙O的切线；

（2）∵

∴设，，

∵∠ACB＝90°

∴，

∵AB、AC是⊙O的切线，

∴

∴，

∵，=90°，

∴∽，

∴，即，

∴，

∴，，

∴；

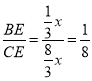（3）连接CD．

由（2）得CE＝＝2×4，

解得＝3，

∴AC＝12，BC＝9，

∴AO，

AD＝AO﹣OD＝4﹣4，

∵CE是O的直径，

∴∠CDE=90°，

∵∠ACB=90°，

∴∠CDE=∠ACB=90°，

∴∠CED+∠ECD=∠ECD+∠ACD=90°，

∴∠CED=∠ACD，

∵OD=OE，

∴∠CED=∠ODE，

又∵∠ODE=∠ADF，

∴∠ADF=∠ACD，

又∵∠DAF=∠CAD

∴△DFA∽△CDA，

∴，

即，

解得 AF，

CF12﹣，

∴，

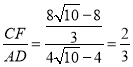故求得的值为．