Question

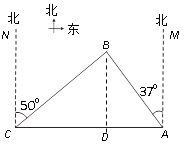
【题目】如图：锐角△ABC中，∠C＝2∠B，AD是高，求证：AC+CD＝BD．

线段和差，通常用截长或补短法证明，下面是甲、乙两位同学的思路，请你按他们的思路，给出一种证明．

甲：截长法，在DB上截取DE＝DC，连AE，去证BE＝AC；

乙：补短法，延长DC到E，使CE＝CA，连接AE，去证DB＝DE．

Answer 1

【答案】见解析.

【解析】

甲：由线段垂直平分线的性质可得AE=AC，由等腰三角形的性质可得∠AEC=∠C，由外角性质可得∠B=∠BAE，可得AE=BE=AC，即可得结论；

乙：由外角性质可得∠ACB=2∠E，可得∠B=∠E，可得AB=AE，由等腰三角形的性质可得BD=DE，即可得结论．

解：甲：截长法，如图1，在DB上截取DE＝DC，连AE，

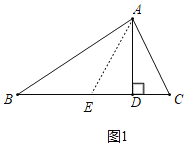
∵DE＝DC，AD⊥BC，

∴AE＝AC，

∴∠AEC＝∠C，且∠C＝2∠B，

∴∠AEC＝∠B，且∠AEC＝∠B+∠BAE，

∴∠B＝∠BAE，

∴AE＝BE＝AC，

∴BD＝BE+DE＝AC+CD

乙：补短法，延长DC到E，使CE＝CA，连接AE，

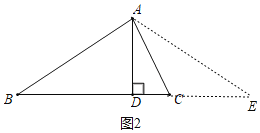
∵CE＝CA，

∴∠E＝∠CAE，且∠ACB＝∠E+∠CAE，

∴∠ACB＝2∠E，且∠ACB＝2∠B，

∴∠B＝∠E，

∴AB＝AE，且AD⊥BC，

∴BD＝DE，

∵DE＝DC+CE＝AC+DC，

∴BD＝DC+AC．