题目内容
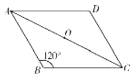
【题目】如图,平行四边形![]() 中,连接
中,连接![]() ,点
,点![]() 为对称中心,点
为对称中心,点![]() 在
在![]() 上,若
上,若![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ______.
______.
【答案】![]() 或2
或2![]()
【解析】
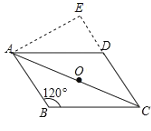
首先过点A作AE⊥CD,交CD的延长线于点E,由平行四边形ABCD中,∠ABC=120°,BC=2![]() ,可求得AE的长,又由tan∠DCA=
,可求得AE的长,又由tan∠DCA=![]() ,可求得AC的长,然后分别从点P在OA上与点P在OC上去分析求解即可求得答案.
,可求得AC的长,然后分别从点P在OA上与点P在OC上去分析求解即可求得答案.
过点A作AE⊥CD,交CD的延长线于点E,
∵四边形ABCD是平行四边形,∠ABC=120°,BC=2![]() ,
,
∴∠ADC=∠ABC=120°,AD=BC=2![]() ,
,
∴∠ADE=60°,
∴∠EAD=30°,
∴ED=![]() AD=
AD=![]() ,
,
∴AE=![]() =3,
=3,
∵tan∠DCA=![]() ,
,
∴EC=2AE=6,
∴AC=![]() =3
=3![]() ,
,
∴OA=![]() AC=
AC=![]() ,
,
若点P在OA上,则AP=OAOP=![]() -
-![]() =
=![]() ;
;
若点P在OC上,AP=OA+OP=![]() +
+![]() =2
=2![]() .
.
∴AP=![]() 或2
或2![]() .
.
故答案为:![]() 或2
或2![]() .
.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目