题目内容
【题目】甲乙两个工厂同时加工一批机器零件.甲工厂先加工了两天后停止加工,维修设备,当维修完设备时,甲乙两厂加工的零件数相等,甲工厂再以原来的工作效率继续加工这批零件.甲乙两厂加工零件的数量y甲(件),y乙(件)与加工件的时间x(天)的函数图象如图所示,
(1)乙工厂每天加工零件的数为 件;
(2)甲工厂维修设备的时间是多少天?
(3)求甲维修设备后加工零件的数量y甲(件)与加工零件的时间x(天)的函数关系式,并写出自变量x的取值范围.
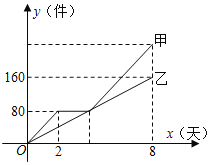
【答案】(1)20;(2)甲工厂维修设备的时间为2天.(3)y甲=40x﹣80(4≤x≤8).
【解析】
(1)根据函数图像知,乙8天加工160件,从而求得每天加工件数;
(2)根据乙的解析式,求出甲完成维修后的时间,减去刚开始的2天即为维修时间;
(3)第(2)问已求得k=40,利用维修完成时刻的坐标点代入函数,可得b的值,从而得出解析式.
解:(1)160÷8=20(件),
即乙工厂每天加工零件的数为20件;
故答案为:20.
(2)∵y甲=20x,
∴当y=80时,x=4,
∴4﹣2=2(天),
∴甲工厂维修设备的时间为2天.
(3)∵甲的工作效率为![]() (件/天),
(件/天),
∴设y甲=40x+b.
∵过点(4,80),
∴40×4+b=80,
∴b=﹣80,
∴y甲=40x﹣80(4≤x≤8).

 轻巧夺冠周测月考直通名校系列答案
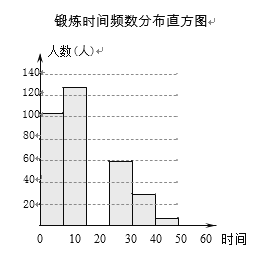
轻巧夺冠周测月考直通名校系列答案【题目】某数学活动小组为了解全县九年级学生在抗新冠病毒疫情期间平均每天居家锻炼时间,向全县部分学生进行了抽样调查,并将收集到的数据整理成如图的统计图(部分数据未标出).
(1)这次抽样调查的学生人数一共有 人;
(2)求频数分布表中 a 的值,并补全频数分布直方图; ,
(3)若该县有 5000 名九年级学生,请你估计全县九年级学生平均每天居家锻炼时间不超过20分钟的有多少人?
时间 x/分 | 人数/人 | 频率 |
0<x≤10 | 102 | 25.5% |
10<x≤20 | 132 | 33% |
20<x≤30 | a | 17.5% |
30<x≤40 | 59 | 14.75% |
40<x≤50 | 29 | 7.25% |
50<x≤60 | 8 | 2% |