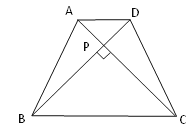
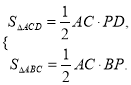题目内容
【题目】如图，平面直角坐标系中O是原点，ABCD的顶点A，C的坐标分别是（8，0），（3，4），点D，E把线段OB三等分，延长CD、CE分别交OA、AB于点F，G，连接FG．则下列结论：
①F是OA的中点；②△OFD与△BEG相似；③四边形DEGF的面积是 
；④OD= 
其中正确的结论是（填写所有正确结论的序号）．
【答案】②③
【解析】解：①∵四边形OABC是平行四边形，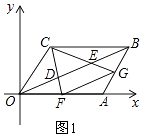
∴BC∥OA，BC=OA，
∴△CDB∽△FDO，
∴ 
，
∵D、E为OB的三等分点，
∴ 
= 
，
∴ 
，
∴BC=2OF，
∴OA=2OF，
∴F是OA的中点；
所以①结论正确；②如图2，延长BC交y轴于H，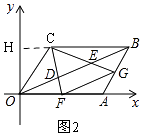
由C（3，4）知：OH=4，CH=3，
∴OC=5，
∴AB=OC=5，
∵A（8，0），
∴OA=8，
∴OA≠AB，
∴∠AOB≠∠EBG，
∴△OFD∽△BEG不成立，
所以②结论不正确；③由①知：F为OA的中点，
同理得；G是AB的中点，
∴FG是△OAB的中位线，
∴FG= 
，FG∥OB，
∵OB=3DE，
∴FG= 
DE，
∴ 
= ，
过C作CQ⊥AB于Q，
SOABC=OAOH=ABCQ，
∴4×8=5CQ，
∴CQ= 
，
S△OCF= 
OFOH= ×4×4=8，
S△CGB= BGCQ= × 
× =8，
S△AFG= ×4×2=4，
∴S△CFG=SOABC﹣S△OFC﹣S△OBG﹣S△AFG=8×4﹣8﹣8×4=12，
∵DE∥FG，
∴△CDE∽△CFG，
∴ 
= 
= 
，
∴ 
= 
，
∴ 
，
∴S四边形DEGF= 
；
所以③结论正确；④在Rt△OHB中，由勾股定理得：OB2=BH2+OH2 ，
∴OB= 
= 
，
∴OD= 
，
所以④结论不正确；
故本题结论正确的有：②③；
所以答案是：②③．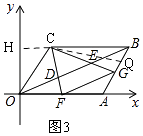
【考点精析】认真审题，首先需要了解勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2)，还要掌握相似三角形的判定与性质(相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方)的相关知识才是答题的关键．
