Question

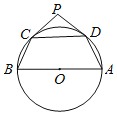
【题目】如图，AB是⊙O的直径，C、D为⊙O上的点，P为圆外一点，PC、PD均与圆相切，设∠A+∠B＝130°，∠CPD＝β，则β＝_____．

Answer 1

【答案】100°

【解析】

连结OC，OD，则∠PCO＝90°，∠PDO＝90°，可得∠CPD＋∠COD＝180°，根据OB＝OC，OD＝OA，可得∠BOC＝180°2∠B，∠AOD＝180°2∠A，则可得出与β的关系式．进而可求出β的度数．

连结OC，OD，

∵PC、PD均与圆相切，

∴∠PCO＝90°，∠PDO＝90°，

∵∠PCO+∠COD+∠ODP+∠CPD＝360°，

∴∠CPD+∠COD＝180°，

∵OB＝OC，OD＝OA，

∴∠BOC＝180°﹣2∠B，∠AOD＝180°﹣2∠A，

∴∠COD+∠BOC+∠AOD＝180°，

∴180°﹣∠CPD+180°﹣2∠B+180°﹣2∠A＝180°．

∴∠CPD＝100°，

故答案为：100°．