题目内容
【题目】如图，在矩形ABCD中，点E是AD上的一个动点，连接BE，作点A关于BE的对称点F，且点F落在矩形ABCD的内部，连接AF，BF，EF，过点F作GF⊥AF交AD于点G，设
．
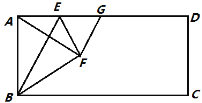
（1）求证：AE=GE；
（2）当点F落在AC上时，用含n的代数式表示
的值；
（3）若AD=4AB，且以点F，C，G为顶点的三角形是直角三角形，求n的值．
【答案】（1）证明见解析；（2）
=
；（3）n=16或 
．
【解析】
试题分析：（1）因为GF⊥AF，由对称易得AE=EF，则由直角三角形的两个锐角的和为90度，且等边对等角，即可证明E是AG的中点；（2）可设AE=a，则AD=na，即需要用n或a表示出AB，由BE⊥AF和∠BAE==∠D=90°，可证明△ABE~△DAC ， 则
，因为AB=DC，且DA，AE已知表示出来了，所以可求出AB，即可解答；（3）求以点F，C，G为顶点的三角形是直角三角形时的n，需要分类讨论，一般分三个，∠FCG=90°，∠CFG=90°，∠CGF=90°；根据点F在矩形ABCD的内部就可排除∠FCG=90°，所以就以∠CFG=90°和∠CGF=90°进行分析解答．
试题解析：（1）证明：由对称得AE=FE，∴∠EAF=∠EFA，∵GF⊥AE，∴∠EAF+∠FGA=∠EFA+∠EFG=90°，∴∠FGA=∠EFG，∴EG=EF，∴AE=EG．
（2）解：设AE=a，则AD=na，当点F落在AC上时（如图1），由对称得BE⊥AF，∴∠ABE+∠BAC=90°，∵∠DAC+∠BAC=90°，∴∠ABE=∠DAC，又∵∠BAE=∠D=90°，∴△ABE~△DAC ，∴
∵AB=DC，∴AB2=AD·AE=na·a=na2，∵AB>0，∴AB=
，∴=
=，∴=.
（3）解：设AE=a，则AD=na，由AD=4AB，则AB=
.
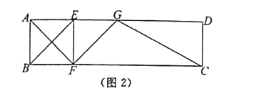
当点F落在线段BC上时（如图2），EF=AE=AB=a，此时
，∴n=4，∴当点F落在矩形外部时，n>4．
∵点F落在矩形的内部，点G在AD上，∴∠FCG<∠BCD，∴∠FCG<90°，若∠CFG=90°，则点F落在AC上，由（2）得=，∴n=16．
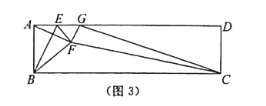
若∠CGF=90°（如图3），则∠CGD+∠AGF=90°，∵∠FAG+∠AGF=90°，∴∠CGD=∠FAG=∠ABE，∵∠BAE=∠D=90°，∴△ABE~△DGC，∴ 
，∴AB·DC=DG·AE，即
.
解得 n=或n=
＜4（不合题意，舍去），∴当n=16或 时，以点F，C，G为顶点的三角形是直角三角形．
