ЬтФПФкШн
ЁОЬтФПЁПаТЖЈвхЃКЖдгкЙигк![]() ЕФКЏЪ§
ЕФКЏЪ§![]() ЮвУЧГЦКЏЪ§
ЮвУЧГЦКЏЪ§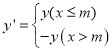 ЮЊКЏЪ§
ЮЊКЏЪ§![]() ЕФ
ЕФ![]() ЗжКЏЪ§(Цфжа
ЗжКЏЪ§(Цфжа![]() ЮЊГЃЪ§)ЃЎ
ЮЊГЃЪ§)ЃЎ
Р§ШчЃКЖдгкЙигк![]() ЕФвЛДЮКЏЪ§
ЕФвЛДЮКЏЪ§![]() ЕФ
ЕФ![]() ЗжКЏЪ§ЮЊ
ЗжКЏЪ§ЮЊ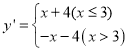
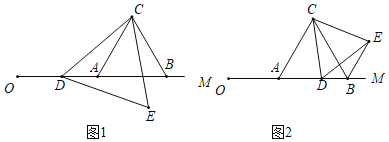
ЃЈ1ЃЉШєЕу![]() дкЙигк
дкЙигк![]() ЕФвЛДЮКЏЪ§
ЕФвЛДЮКЏЪ§![]() ЕФ
ЕФ![]() ЗжКЏЪ§ЩЯЃЌЧѓ
ЗжКЏЪ§ЩЯЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ЃЈ2ЃЉаДГіЗДБШР§КЏЪ§![]() ЕФ
ЕФ![]() ЗжКЏЪ§ЕФЭМЯѓЩЯ
ЗжКЏЪ§ЕФЭМЯѓЩЯ![]() Ыц
Ыц![]() ЕФдіДѓЖјМѕаЁЕФ
ЕФдіДѓЖјМѕаЁЕФ![]() ЕФШЁжЕЗЖЮЇ ЃЛ
ЕФШЁжЕЗЖЮЇ ЃЛ
ЃЈ3ЃЉШє![]() ЪЧЖўДЮКЏЪ§
ЪЧЖўДЮКЏЪ§![]() Йигк
Йигк![]() ЕФ
ЕФ![]() ЗжКЏЪ§ЃЎ
ЗжКЏЪ§ЃЎ
![]() ЕБ
ЕБ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
![]() ЕБ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() дђ
дђ![]() ЕФШЁжЕЗЖЮЇЮЊ ЃЛ
ЕФШЁжЕЗЖЮЇЮЊ ЃЛ
ЃЈ4ЃЉШєЕу![]() СЌНс
СЌНс![]() ЕБЙигк
ЕБЙигк![]() ЕФЖўДЮКЏЪ§
ЕФЖўДЮКЏЪ§![]() ЕФ
ЕФ![]() ЗжКЏЪ§ЃЌгыЯпЖЮ
ЗжКЏЪ§ЃЌгыЯпЖЮ![]() гаСНИіНЛЕуЃЌжБНгаДГі
гаСНИіНЛЕуЃЌжБНгаДГі![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЈ2ЃЉ
ЃЈ2ЃЉ![]() Лђ
Лђ![]() ЃЈ3ЃЉЂй
ЃЈ3ЃЉЂй![]() Лђ
Лђ![]() Ђк
Ђк![]() ЃЈ4ЃЉmЃМ1Лђ
ЃЈ4ЃЉmЃМ1Лђ![]() ЁмmЃМ
ЁмmЃМ![]() ЛђmЁн4
ЛђmЁн4
ЁОНтЮіЁП
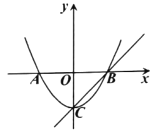
ЃЈ1ЃЉИљОнЬтвтаДГівЛДЮКЏЪ§yЃНxЃЋ1ЕФ2ЗжКЏЪ§ЮЊy'ЃЌАбx=4ДњШыМДПЩЧѓНтЃЛ
ЃЈ2ЃЉИљОнЬтвтаДГіЗДБШР§КЏЪ§![]() ЕФ
ЕФ![]() ЗжКЏЪ§y'ЃЌИљОнЗДБШР§КЏЪ§ЕФЭМЯёМДПЩХаЖЯЃЛ
ЗжКЏЪ§y'ЃЌИљОнЗДБШР§КЏЪ§ЕФЭМЯёМДПЩХаЖЯЃЛ
ЃЈ3ЃЉЂйИљОнЬтвтаДГіЖўДЮКЏЪ§![]() Йигк
Йигк![]() ЕФ
ЕФ![]() ЗжКЏЪ§y'ЃЌИљОн
ЗжКЏЪ§y'ЃЌИљОн![]() ЗжЖЮМДПЩЧѓНтЃЛ
ЗжЖЮМДПЩЧѓНтЃЛ
ЂкЪзЯШЧѓГіЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЕФШЁжЕЗЖЮЇЮЊ
ЕФШЁжЕЗЖЮЇЮЊ![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ПЩжЊЃЌЧѓГі
ПЩжЊЃЌЧѓГі![]() ЪБ
ЪБ![]() ЕФжЕдк-3КЭ-4ЃЈАќКЌ-3КЭ-4ЃЉжЎМфЖдгІЕФxЕФШЁжЕЗЖЮЇМДПЩЃЛ
ЕФжЕдк-3КЭ-4ЃЈАќКЌ-3КЭ-4ЃЉжЎМфЖдгІЕФxЕФШЁжЕЗЖЮЇМДПЩЃЛ
ЃЈ4ЃЉЯШаДГіЖўДЮКЏЪ§![]() Йигк
Йигк![]() ЕФmЗжКЏЪ§y'ЃЌЕБx23x3ЃН1ЪБЃЌxЃН1ЛђxЃН4ЃЌЕБx2ЃЋspan>3xЃЋ3ЃН1ЪБЃЌxЃН
ЕФmЗжКЏЪ§y'ЃЌЕБx23x3ЃН1ЪБЃЌxЃН1ЛђxЃН4ЃЌЕБx2ЃЋspan>3xЃЋ3ЃН1ЪБЃЌxЃН![]() ЛђxЃН
ЛђxЃН![]() ЃЌЕБyЃНx23x3гыЯпЖЮABУЛгаНЛЕуЃЌmЃМ1ЃЛЕБyЃНx23x3гыЯпЖЮABгавЛИіНЛЕуЃЌyЃНx2ЃЋ3xЃЋ3гыЯпЖЮABгавЛИіНЛЕуЃЌ
ЃЌЕБyЃНx23x3гыЯпЖЮABУЛгаНЛЕуЃЌmЃМ1ЃЛЕБyЃНx23x3гыЯпЖЮABгавЛИіНЛЕуЃЌyЃНx2ЃЋ3xЃЋ3гыЯпЖЮABгавЛИіНЛЕуЃЌ![]() ЃМmЃМ
ЃМmЃМ![]() ЃЛЕБyЃНx23x3гыЯпЖЮABгаСНИіНЛЕуЃЌmЁн4ЃЎ
ЃЛЕБyЃНx23x3гыЯпЖЮABгаСНИіНЛЕуЃЌmЁн4ЃЎ
ЃЈ1ЃЉвЛДЮКЏЪ§yЃНxЃЋ1ЕФ2ЗжКЏЪ§ЮЊ![]()
![]()
![]() Аб
Аб![]() ДњШы
ДњШы![]() ЕУ
ЕУ![]()
![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЗДБШР§КЏЪ§![]() ЕФ4ЗжКЏЪ§ЮЊ
ЕФ4ЗжКЏЪ§ЮЊ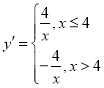 ЃЌ
ЃЌ
ЁрyЫцxЕФдіДѓЖјМѕаЁЪБЃЌ![]() Лђ
Лђ![]() ЃЛ
ЃЛ
ЙЪД№АИЮЊЃК![]() Лђ
Лђ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЖўДЮКЏЪ§yЃНx22x3ЙигкxЕФ1ЗжКЏЪ§ЮЊ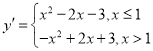
ЂйЕБ1ЁмxЁм2ЪБЃЌ
1ЁмxЁм1ЃЌy'=![]() ЃЌyЕФШЁжЕЗЖЮЇЮЊ4Ёмy'Ём0ЃЌ
ЃЌyЕФШЁжЕЗЖЮЇЮЊ4Ёмy'Ём0ЃЌ
1ЃМxЁм2ЃЌy'=![]() ЃЌyЕФШЁжЕЗЖЮЇЮЊ3Ёмy'ЃМ4ЃЌ
ЃЌyЕФШЁжЕЗЖЮЇЮЊ3Ёмy'ЃМ4ЃЌ
ЁрЕБ1ЁмxЁм2ЪБЃЌy'ЕФШЁжЕЗЖЮЇЮЊ4Ёмy'Ём0ЃЌ3Ёмy'ЃМ4ЃЛ
Ђкimg src="http://thumb.zyjl.cn/questionBank/Upload/2020/11/27/15/1b1ac277/SYS202011271558349761366940_DA/SYS202011271558349761366940_DA.033.png" width="15" height="13" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />Аб![]() ДњШы
ДњШы![]() ПЩЕУ
ПЩЕУ![]()
Аб![]() ДњШы
ДњШы![]() ПЩЕУ
ПЩЕУ![]()
![]() ЕБ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЕФШЁжЕЗЖЮЇЮЊ
ЕФШЁжЕЗЖЮЇЮЊ![]()
гЩЂйжЊЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]()
Аб![]() ДњШы
ДњШы![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЌ
ЃЌ![]() ЃЈЩсШЅЃЉ
ЃЈЩсШЅЃЉ
Аб![]() ДњШы
ДњШы![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ![]() ЃЈЩсШЅЃЉ
ЃЈЩсШЅЃЉ
![]() kЕФШЁжЕЗЖЮЇЮЊЃК
kЕФШЁжЕЗЖЮЇЮЊЃК![]()
ЃЈ4ЃЉЖўДЮКЏЪ§yЃНx23x3ЕФmЗжКЏЪ§ЮЊ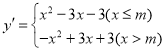
ЕБx23x3ЃН1ЪБЃЌxЃН1ЛђxЃН4ЃЌ
ЕБx2ЃЋ3xЃЋ3ЃН1ЪБЃЌx=![]() ЛђxЃН
ЛђxЃН![]() ЃЌ
ЃЌ
ЕБyЃНx23x3гыЯпЖЮABУЛгаНЛЕуЃЌmЃМ1ЃЛ
ЕБyЃНx23x3гыЯпЖЮABгавЛИіНЛЕуЃЌyЃНx2ЃЋ3xЃЋ3гыЯпЖЮABгавЛИіНЛЕуЃЌ
Ёр![]() ЁмmЃМ
ЁмmЃМ![]() ЃЛ
ЃЛ
ЕБyЃНx23x3гыЯпЖЮABгаСНИіНЛЕуЃЌmЁн4ЃЛ
злЩЯЫљЪіЃКmЃМ1Лђ![]() ЁмmЃМ
ЁмmЃМ![]() ЛђmЁн4ЃЎ
ЛђmЁн4ЃЎ

 ПЮЪБеЦПиЫцЬУСЗЯАЯЕСаД№АИ
ПЮЪБеЦПиЫцЬУСЗЯАЯЕСаД№АИ вЛПЮвЛСЗвЛБОЭЈЯЕСаД№АИ
вЛПЮвЛСЗвЛБОЭЈЯЕСаД№АИ еуНжЎаЧбЇвЕЫЎЦНВтЪдЯЕСаД№АИ
еуНжЎаЧбЇвЕЫЎЦНВтЪдЯЕСаД№АИ