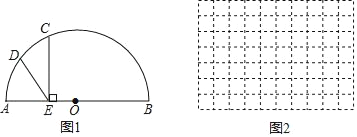��Ŀ����
����Ŀ���Ķ����ϣ���֪ʵ��m��n����![]() ����
����![]() ��ֵ��
��ֵ��
�⣺��![]() ����ԭ���̿ɻ�Ϊ(t+1)(t-1)=35��������t2-1=35��t2=36��
����ԭ���̿ɻ�Ϊ(t+1)(t-1)=35��������t2-1=35��t2=36��
��t=��6��
��![]() ��
��
��![]()
�������ֽ��ⷽ��Ϊ����Ԫ�������ڽṹ�ϸ��ӵ�����ʽ�������У���������ijЩ���ֿ���һ�����壬����ʹ���ӵ����������������Ԫ��������������⣺
��1����֪ʵ��x��y����![]() ����
����![]() ��ֵ��
��ֵ��
��2�����ĸ������������Ļ�Ϊ360�������ĸ���������������
���𰸡���1��![]() ����2�����ĸ��������������ֱ���3��4��5��6��
����2�����ĸ��������������ֱ���3��4��5��6��
��������
��1����![]() ��ԭ���̿ɻ�Ϊ
��ԭ���̿ɻ�Ϊ![]() ����⼴�ã�
����⼴�ã�
��2������С��������Ϊ![]() �������������������ֱ�Ϊ
�������������������ֱ�Ϊ![]() ��
��![]() ��
��![]() ���ɸ�������ó�
���ɸ�������ó�![]() ������Ϊ
������Ϊ![]() ������
������![]() ������ԪΪ����
������ԪΪ����![]() ��һԪ���η�����⣬�����ٽ����
��һԪ���η�����⣬�����ٽ����![]() �ķ��̼��ã�
�ķ��̼��ã�
�⣺��1����![]() ��
��
��ԭ���̿ɻ�Ϊ![]() ��
��
������![]() ��
��
���![]() ��
��
��![]() ��
��
��![]()
��![]() ��
��
��2������С��������Ϊ![]() �������������������ֱ�Ϊ
�������������������ֱ�Ϊ![]() ��
��![]() ��
��![]() ��
��
��������ã�![]() ��
��
![]() ��
��
![]() ��
��
��![]() ����ԭ����Ϊ
����ԭ����Ϊ![]() ��
��
������![]() ��
��
��![]()
��![]()
��![]() ����
����![]() ��
��![]() ��
��
��![]() ����
����![]() ����
����![]() ��
��
��![]() �����
�����![]() ��
��![]() ����ȥ����
����ȥ����
�����ĸ��������������ֱ���3��4��5��6��

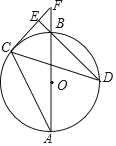
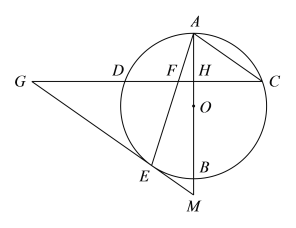
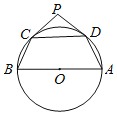
����Ŀ����ͼ��AB�ǡ�O��ֱ����C��DΪ��O�ϵĵ㣬PΪԲ��һ�㣬PC��PD����Բ���У����A+��B��130�㣬��CPD������������_____��
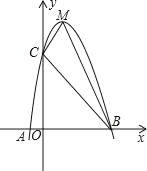
����Ŀ�� ֣��ij�̳�������һ����ͯ�ڹ���һ����ͯ������ߣ���֪��������ʱ����20Ԫ�����鷢�֣�����ߵ���������y�����������۵���x��Ԫ��֮������һ�κ�����ϵ���±����������������۵��۵ļ����Ӧ��ϵ��
�����۵���x/Ԫ | 30 | 35 | 40 | 45 |
��������y/�� | 230 | 180 | 130 | m |
��1����y��x�ĺ�����ϵʽ��
��2������������Ϣ��գ�
��m=______��
�ڵ����۵���x=______Ԫʱ������������������������______Ԫ��
��3��������۲��Ź涨��ÿ������ۼ۲��ܸ���40Ԫ����������������2520Ԫ���������۵���x��ȡֵ��Χ��
����Ŀ��ij�����ڳ�����һ�����������壬���¶Ȳ���ʱ���������������ѹp����λ��ǧ�������������V����λ�������ף��ı仯���仯��p��V�ı仯��������ʾ��
P | 1.5 | 2 | 2.5 | 3 | 4 | �� |
V | 64 | 48 | 38.4 | 32 | 24 | �� |
��1��д��һ�����ϱ������ݵ�p����V�ĺ�������ʽ�� ��
��2���������ڵ���ѹ����144ǧ��ʱ������ը�����գ�1���еĺ�������ʽ�����ڰ�ȫ���ǣ�������������Ϊ���������ף�
����Ŀ����ͼ1��ABΪ��ԲO��ֱ�����뾶�ij�Ϊ4cm����CΪ��Բ��һ���㣬����C��CE��AB������Ϊ��E����DΪ��AC���е㣬����DE�����DE=2OE�����߶�AE�ij���
С�θ���ѧϰ�����ľ��飬��������ת��Ϊ������������
С������AE�ij���Ϊxcm���߶�DE�ij���Ϊycm��
������C���A�غ�ʱ��AE�ij���Ϊ0cm�����Ժ���y���Ա���x�ı仯���仯�Ĺ��ɽ���̽����
������С�ε�̽�����̣��벹����������˵����������ݱ���һλС������
��1��ͨ��ȡ�㡢��ͼ���������õ���x��y�ļ���ֵ�����±���
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
y/cm | 0 | 1.6 | 2.5 | 3.3 | 4.0 | 4.7 | �� �� | 5.8 | 5.7 |
��x=6cmʱ��������ͼ�а���С�������ͼ����ʹ�ÿ̶ȳ߶�����ʱ�߶�DE�ij��ȣ���д�ڱ���հ״���
��2����ͼ2�н���ƽ��ֱ������ϵ�������ȫ��ı��и����ӦֵΪ����ĵ㣬�����ú�����ͼ����
��3����ϻ����ĺ���ͼ�������⣬��DE=2OEʱ��AE�ij���ԼΪ�� ��cm��