题目内容
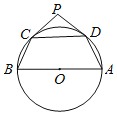
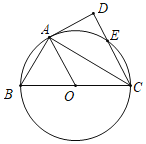
【题目】如图,已知BC是⊙O的直径,AD切⊙于点A,CD∥OA交⊙O于另一点E.
(1)求证:△ACD∽△BCA;
(2)若A是⊙O上一动点,则
①当∠B=_____时,以A,O,C,D为顶点的四边形是正方形;
②当∠B=_____时,以A,O,C,E为顶点的四边形是菱形.
【答案】(1)详见解析;(2)①45°;②60°
【解析】
(1)证明∠BAC=∠ADC与∠ACD=∠ACO,即可证明△ACD∽△BCA;
(2)①当∠B=45°时,以A,O,C,D为顶点的四边形是正方形;②当∠B=60°时,以A,O,C,D为顶点的四边形是棱形.
解:(1)证明:∵AD 切⊙O 于点 A,
∴OA⊥AD,
∵CD∥OA,
∴∠ADC=90°,
∵BC 是⊙O 的直径,
∴∠BAC=90°,
∴∠BAC=∠ADC,
又∵CD∥OA,
∴∠ACD=∠CAO,
∵OA=OC,
∴∠ACO=∠CAO,
∴∠ACD=∠ACO,
∴△ACD∽△BCA;
(2)①∵四边形AOCD为正方形,
∴∠AOC=90°,
∵OA=OC,
∠OCA=∠OAC=45°,
∵∠BAC=90°,
∴∠B=90°﹣45°=45°,
故答案为45°;
②连接AE,
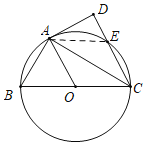
∵AD为切线,
∴∠DAE=∠ECA,∠OAD=90°
∵四边形AOCE为菱形,
∠OAC=∠EAC,
∴∠DAE=∠ECA=∠OAC=30°
∴∠ACO=30°,
∴∠AOB=∠ACO+∠OAC=30°+30°=60°
∵OA=OB,
∴∠B=60°.
故答案为 60°.

 华东师大版一课一练系列答案
华东师大版一课一练系列答案【题目】 郑州某商场在“六一”儿童节购进一批儿童智力玩具.已知成批购进时单价20元,调查发现:该玩具的月销售量y(个)与销售单价x(元)之间满足一次函数关系,下表是月销售量、销售单价的几组对应关系:
月销售单价x/元 | 30 | 35 | 40 | 45 |
月销售量y/个 | 230 | 180 | 130 | m |
(1)求y与x的函数关系式;
(2)根据以上信息填空:
①m=______;
②当销售单价x=______元时,月销售利润最大,最大利润是______元;
(3)根据物价部门规定,每件玩具售价不能高于40元,若月销售利润不低于2520元,试求销售单价x的取值范围.
【题目】某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(单位:千帕)随气体体积V(单位:立方米)的变化而变化,p随V的变化情况如表所示.
P | 1.5 | 2 | 2.5 | 3 | 4 | … |
V | 64 | 48 | 38.4 | 32 | 24 | … |
(1)写出一个符合表格数据的p关于V的函数解析式
(2)当气球内的气压大于144千帕时,气球将爆炸,依照(1)中的函数解析式,基于安全考虑,气球的体积至少为多少立方米?