题目内容

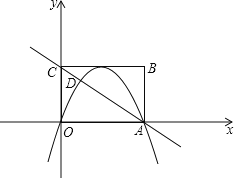
【题目】如图，在以O为原点的直角坐标系中，点A，C分别在x轴、y轴的正半轴上，点B在第一象限内，四边形OABC是矩形，反比例函数y＝（x＞0）与AB相交于点D，与BC相交于点E，若BE＝4CE，四边形ODBE的面积是8，则k＝_____．

【答案】2

【解析】

利用反比例函数图象上点的坐标特征，设E（a，），利用BE=4CE得到B（5a，），根据反比例函数比例系数k的几何意义，利用四边形ODBE的面积=S矩形ABCO-S△OCE-S△AOD得到5a-k-k=8，然后解方程即可．

设E（a，），

∵BE=4CE，

∴B（5a，），

∵四边形ODBE的面积=S矩形ABCO-S△OCE-S△AOD，

∴5a-k-k=8，

解得k=2．

故答案为2．

练习册系列答案
相关题目

【题目】国家推行“节能减排，低碳经济”政策后，低排量的汽车比较畅销，某汽车经销商购进A、B两种型号的低排量汽车，其中A型汽车的进货单价比B型汽车的进货单价多2万元；花50万元购进A型汽车的数量与花40万元购进B型汽车的数量相同．

（1）求A、B两种型号汽车的进货单价；

（2）销售中发现A型汽车的每周销量yA（台）与售价x（万元/台）满足函数关系yA＝﹣x+20，B型汽车的每周销量yB（台）与售价x（万元/台）满足函数关系yB＝﹣x+14，A型汽车的售价比B型汽车的售价高2万元/台．问A、B两种型号的汽车售价各为多少时，每周销售这两种汽车的总利润最大？最大利润是多少万元？

【题目】如图，在正方形ABCD中，DC=8，现将四边形BEGC沿折痕EG(G，E分别在DC，AB边上)折叠，其顶点B，C分别落在边AD上和边DC的上部，其对应点设为F，N点，且FN交DC于M．

特例体验：

(1)当FD=AF时，△FDM的周长是多少?

类比探究：

(2)当FD≠AF≠0时，△FDM的周长会发生变化吗?请证明你的猜想．

拓展延伸：

(3)同样在FD≠AF≠0的条件下，设AF为x，被折起部分(即：四边形FEGN)的面积为S，试用含x的代数式表示S，并问：当x为何值时，S=26?

【题目】某市场将进货价为40元/件的商品按60元/件售出，每星期可卖出300件．市场调查反映：如调整价格，每涨价1元/件，每星期该商品要少卖出10件．

（1）请写出该商场每月卖出该商品所获得的利润y（元）与该商品每件涨价x（元）间的函数关系式；

（2）每月该商场销售该种商品获利能否达到6300元？请说明理由；

（3）请分析并回答每件售价在什么范围内，该商场获得的月利润不低于6160元？

【题目】为弘扬中华传统文化，我市某中学决定根据学生的兴趣爱好组建课外兴趣小组，因此学校随机抽取了部分同学的兴趣爱好进行调查，将收集的数据整理并绘制成下列两幅统计图，请根据图中的信息，完成下列问题：

（1）学校这次调查共抽取了　 　名学生；

（2）补全条形统计图；

（3）在扇形统计图中，“戏曲”所在扇形的圆心角度数为　 　；

（4）设该校共有学生2000名，请你估计该校有多少名学生喜欢书法？

【题目】某校计划一次性购买排球和篮球，每个篮球的价格比排球贵30元；购买2个排球和3个篮球共需340元．

(1)求每个排球和篮球的价格：

(2)若该校一次性购买排球和篮球共60个，总费用不超过3800元，且购买排球的个数少于39个．设排球的个数为m，总费用为y元．

①求y关于m的函数关系式，并求m可取的所有值；

②在学校按怎样的方案购买时，费用最低？最低费用为多少？

【题目】如图，反比例函数y=（x＞0）过点A（3，4），直线AC与x轴交于点C（6，0），过点C作x轴的垂线BC交反比例函数图象于点B.

（1）求k的值与B点的坐标；

（2）在平面内有点D，使得以A，B，C，D四点为顶点的四边形为平行四边形，试写出符合条件的所有D点的坐标.

【题目】如图，矩形OABC在平面直角坐标系xOy中，点A在x轴的正半轴上，点C在y轴的正半轴上，OA=4，OC=3，若抛物线的顶点在BC边上，且抛物线经过O，A两点，直线AC交抛物线于点D．

（1）求抛物线的解析式；

（2）求点D的坐标；

（3）若点M在抛物线上，点N在x轴上，是否存在以A，D，M，N为顶点的四边形是平行四边形？若存在，求出点N的坐标；若不存在，请说明理由．

【题目】如图，为的内接三角形，过点作的切线，交的延长线于，且．

（1）求证：

（2）若，，求的长度．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网