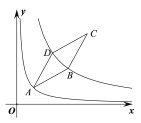
题目内容
【题目】我们知道,三角形的三条角平分线交于一点,这个点称为三角形的内心(即三角形内切圆的圆心) . 现在规定,如果四边形的四条角平分线交于一点,我们把这个点称为“四边形的内心”.
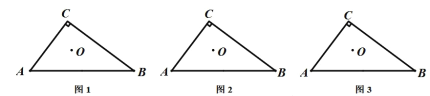
问题提出
(1)如图1,在△ABC中,∠C=90°,点O为△ABC的内心,若直线DE分别交边AC、BC于点D、E,且点O仍然为四边形ABED的内心,这样的直线DE可以画多少条?请在图1中画出一条符合条件的直线DE,并简要说明画法.
问题探究
(2)如图2,在△ABC中,∠C=90°, AC=3, BC=4,若满足(1)中条件的一条直线DE // AB,求此时线段DE的长;
问题解决
(3)如图3,在△ABC中,∠C=90°, AC=3,BC=4,问满足(1)中条件的线段DE是否存在最小值?如果存在,请求出这个值;如果不存在,请说明理由.
【答案】(1)如图1,这样的直线DE可以画无数条;说明画法见解析;(2)DE=![]() ;(3)存在,DE有最小值2
;(3)存在,DE有最小值2![]() -2.
-2.
【解析】
(1)在AC上取点D,连接OD,作∠ODA'=∠ODA,DA'与BC交于点E,通过角平分线的性质定理和逆定理分析判断即可得到直线DE即为所求,所以这样的直线DE有无数条;
(2)由DE // AB,得到△CDE∽△CAB,通过题中数据计算即可;
(3)先求出∠DOE= 45°,然后作△ODE的外接圆⊙O',作O'G⊥DE于点G,连接O'O,O'D, O'E,通过O'O+O'G≥ON,即可得到DE的最小值.
解:(1) 如图1,这样的直线DE可以画无数条.
在AC上取点D,连接OD,作∠ODA'=∠ODA,DA'与BC交于点E,
连接OC;如图2,作OP⊥AC于点P,OQ⊥AB于点Q,ON⊥DE于点N,
由角平分线可知OP=ON=OM,故OE也为∠DEM的平分线,所以直线DE即为所求.
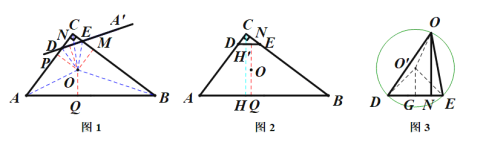
(2)在图1中,由DE//AB,可知N、O、Q共线;作CH⊥AB于点H,交DE于点H'.
由![]() AC·OP+
AC·OP+![]() BC·OM +
BC·OM +![]() AB·OQ=
AB·OQ=![]() AC·BC,有ON =OQ=OM=OP=l;
AC·BC,有ON =OQ=OM=OP=l;
由DE // AB,有∠CDE=∠CAB,∠CED=∠CBA ,
从而△CDE∽△CAB,
故![]() ,
,
即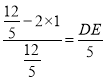 ,
,
解得DE=![]() .
.
(3)存在.
图1中,易知四边形OPCM是正方形,△ODP≌△ODN , △OEM≌△OEN ,
从而可知∠DOE=![]() ∠POM= 45°.
∠POM= 45°.
如图3,作△ODE的外接圆⊙O',作O'G⊥DE于点G,连接O'O,O'D, O'E;
由∠DO'E=2∠DOE=90°,有O'O=O'D=![]() ,O'G=
,O'G=![]() ;
;
由O'O+O'G≥ON,有![]() +
+![]() ≥1,解得DE≥2
≥1,解得DE≥2![]() -2,
-2,
∴DE有最小值2![]() -2.
-2.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案【题目】一次防流感知识检测中,学生得分均为整数,满分10分,成绩达到9分为优秀,这次检测中甲、乙两组学生人数相同,成绩如下两个统计图:
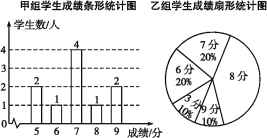
(1)在乙组学生成绩统计图中,8分所在的扇形的圆心角为 度;
(2)请列式计算乙组平均分,补充完整下面的成绩统计分析表所有空格:
平均分 | 方差 | 众数 | 中位数 | 优秀率 | |
甲组 | 7 | 1.8 | 7 | 7 | 20% |
乙组 | 2.6 | 10% |
(3)甲组学生说他们的优秀率高于乙组,所以他们的成绩好于乙组,但乙组学生不同意甲组学生的说法,认为他们组的成绩要好于甲组,请你给出两条支持乙组学生观点的理由.