Question

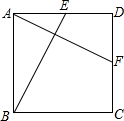
如图，l₁、l₂、l₃、l₄是同一平面内的四条平行直线，且每相邻的两条平行直线间的距离为h，面积是25的正方形ABCD的四个顶点分别在这四条直线上，那么h的值是______．

Answer 1

∵l₁、l₂、l₃、l₄是同一平面内的四条平行直线，且每相邻的两条平行直线间的距离为h，
∴设AE=x，则AD=2x，BE=

5

x，
S_△ABE=

1

2

x•2x=

1

2

•

5

x•h，
解得x=

5

2

h，
AD=2x=

5

h，
∴S_{正方形ABCD}=5h²，
∵正方形ABCD面积是25，
∴5h²=25，
∴h=

5

，
故答案为：

5

．