题目内容
【题目】在平面直角坐标系xOy中,已知二次函数y= ![]() 的图象经过点A(2,0)和点B(1,﹣
的图象经过点A(2,0)和点B(1,﹣ ![]() ),直线l经过抛物线的顶点且与y轴垂直,垂足为Q.
),直线l经过抛物线的顶点且与y轴垂直,垂足为Q.
(1)求该二次函数的表达式;
(2)设抛物线上有一动点P从点B处出发沿抛物线向上运动,其纵坐标y1随时间t(t≥0)的变化规律为y1=﹣ ![]() +2t.现以线段OP为直径作⊙C.
+2t.现以线段OP为直径作⊙C.
①当点P在起始位置点B处时,试判断直线l与⊙C的位置关系,并说明理由;在点P运动的过程中,直线l与⊙C是否始终保持这种位置关系?请说明你的理由.
②若在点P开始运动的同时,直线l也向上平行移动,且垂足Q的纵坐标y2随时间t的变化规律为y2=﹣1+3t,则当t在什么范围内变化时,直线l与⊙C相交?此时,若直线l被⊙C所截得的弦长为a,试求a2的最大值.
【答案】
(1)
解:将点A(2,0)和点B(1,﹣ ![]() )分别代入y=
)分别代入y= ![]() x2+mx+n中,得:
x2+mx+n中,得:
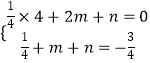 ,
,
解得: ![]() ,
,
∴抛物线的解析式:y= ![]() x2﹣1
x2﹣1
(2)
解:①将P点纵坐标代入(1)的解析式,得:
![]() x2﹣1=﹣
x2﹣1=﹣ ![]() +2t,x=
+2t,x= ![]() ,
,
∴P( ![]() ,﹣
,﹣ ![]() +2t),
+2t),
∴圆心C( ![]() ,﹣
,﹣ ![]() +t),
+t),
∴点C到直线l的距离:﹣ ![]() +t﹣(﹣1)=t+
+t﹣(﹣1)=t+ ![]() ;
;
而OP2=8t+1+(﹣ ![]() +2t)2,得OP=2t+
+2t)2,得OP=2t+ ![]() ,半径OC=t+
,半径OC=t+ ![]() ;
;
∴直线l与⊙C始终保持相切.
②Ⅰ、由①可知,若直线l与⊙C相切,则:2t﹣ ![]() =t+
=t+ ![]() ,t=
,t= ![]() ;
;
∴当0<t< ![]() 时,直线l与⊙C相交;
时,直线l与⊙C相交;
Ⅱ、∵0<t< ![]() 时,圆心C到直线l的距离为d=|2t﹣
时,圆心C到直线l的距离为d=|2t﹣ ![]() |,又半径为r=t+
|,又半径为r=t+ ![]() ,
,
∴a2=4(r2﹣d2)=4[(t+ ![]() )2﹣|2t﹣
)2﹣|2t﹣ ![]() |2]=﹣12t2+15t,
|2]=﹣12t2+15t,
∴t= ![]() 时,a的平方取得最大值为
时,a的平方取得最大值为 ![]()
【解析】(1)所求函数的解析式中有两个待定系数,直接将A、B两点坐标代入即可得解.(2)①由于OP是⊙C的直径,根据P点的纵坐标可表示出C点的纵坐标,进而能表示出C到直线l的距离;OP长易得,然后通过比较⊙C的半径和C到直线l的距离,即可判定直线l与⊙C的位置关系.
②该题要分两问来答,首先看第一问;该小题的思路和①完全一致,唯一不同的地方:要注意直线l与点C的位置关系(需要考虑到C到直线l的表达方式).
在第二问中,a2最大,那么a最大,即直线l被⊙C截得的弦最长,此时圆心C应在直线l上,根据该思路即可得解.
【考点精析】解答此题的关键在于理解二次函数的图象的相关知识,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点,以及对二次函数的性质的理解,了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.

 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案【题目】如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F,⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交⊙O于点H,连接BD、FH.
【题目】为了解某校九年级学生的身高情况,随机抽取部分学生的身高进行调查,利用所得数据绘成如图统计图表:
频数分布表
身高分组 | 频数 | 百分比 |
x<155 | 5 | 10% |
155≤x<160 | a | 20% |
160≤x<165 | 15 | 30% |
165≤x<170 | 14 | b |
x≥170 | 6 | 12% |
总计 | 100% |
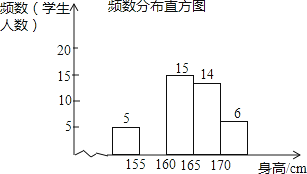
(1)填空:a= , b=;
(2)补全频数分布直方图;
(3)该校九年级共有600名学生,估计身高不低于165cm的学生大约有多少人?