题目内容
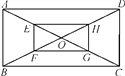
【题目】如图,矩形ABCD的对角线相交于点O,点E,F,G,H分别是AO,BO,CO,DO的中点,请问四边形EFGH是矩形吗?请说明理由.
【答案】见解析
【解析】试题分析:根据四边形ABCD是矩形得知AO=BO=CO=DO,再根据AE=BF=CG=DH,推出OE=OF=OG=OH,证出四边形EFGH为平行四边形,再根据OE=OF=OG=OH得出EG=FH.利用对角线相等且互相平分证出四边形EFGH是矩形.
试题解析:证明:∵四边形ABCD是矩形,
∴AC=BD;AO=BO=CO=DO,(2分)
∵AE=BF=CG=DH,
∴OE=OF=OG=OH,
∴四边形EFGH是平行四边形.
∵OE+OG=FO+OH即EG=FH,
∴四边形EFGH是矩形.

练习册系列答案
相关题目