Question

【题目】已知：数轴上点A、B、C表示的数分别为a、b、c，点O为原点，且a、b、c满足(a﹣6)2+|b﹣2|+|c﹣1|=0．

（1）直接写出a、b、c的值；

（2）如图1，若点M从点A出发以每秒1个单位的速度向右运动，点N从点B出发以每秒3个单位的速度向右运动，点R从点C出发以每秒2个单位的速度向右运动，点M、N、R同时出发，设运动的时间为t秒，t为何值时，点N到点M、R的距离相等；

（3）如图2，若点P从点A出发以每秒1个单位的速度向左运动，点Q从点B出发以每秒3个单位的速度向左运动，点P，Q同时出发开始运动，点K为数轴上的一个动点，且点C始终为线段PK的中点，设运动时间为t秒，若点K到线段PC的中点D的距离为3时，求t的值．

Answer 1

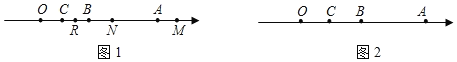
【答案】（1）a=6，b=2，c=1；（2）t为1s时，点N到点M、R的距离相等；（3）t=3或7．

【解析】

（1）根据非负数的性质，列出方程进行解答便可；

（2）先用t的代数式表示NM、NR，再由NM=NR列出t的方程便可；

（3）用t的代数式表示P点，再根据中点公式用t表示D点和K点，再由两点距离公式由DK=3列出t的方程进行解答便可．

（1）∵(a﹣6)2+|b﹣2|+|c﹣1|=0，

∴a﹣6=0，b﹣2=0，c﹣1=0，

∴a=6，b=2，c=1；

（2）由题意得：(6+t)﹣(2+3t)=(2+3t)﹣(1+2t)，

解得：t=1，

∴t为1s时，点N到点M、R的距离相等；

（3）由题意知，P点表示的数为：6﹣t．

∵D是PC的中点，

∴D表示的数为：，

∵C是PK的中点，

∴点K表示的数为：2×1﹣(6﹣t)=t﹣4．

∵KD=3，

∴|(t﹣4)|=3，

∴t=3或7．