题目内容
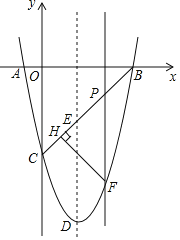
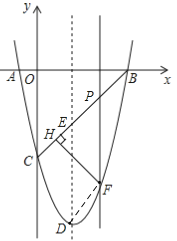
【题目】如图,抛物线y=ax2+bx﹣5与坐标轴交于A(﹣1,0),B(5,0),C(0,﹣5)三点,顶点为D.
(1)请直接写出抛物线的解析式及顶点D的坐标;
(2)连接BC与抛物线的对称轴交于点E,点P为线段BC上的一个动点(点P不与B、C两点重合),过点P作PF∥DE交抛物线于点F,设点P的横坐标为m.
①是否存在点P,使四边形PEDF为平行四边形?若存在,求出点P的坐标;若不存在,说明理由.
②过点F作FH⊥BC于点H,求△PFH周长的最大值.
【答案】(1)y=x2﹣4x﹣5,顶点坐标为D(2,﹣9);(2)①存在点P(3,﹣2)使四边形PEDF为平行四边形;②△PFH周长的最大值为![]() .
.
【解析】(1)利用待定系数法进行求解即可得;
(2)①求出直线BC解析式,表示PF,当PF=DE时,平行四边形存在.
②利用△PFH∽△BCO,应用相似三角形性质表示△PFH周长,应用函数性质讨论最值即可.
(1)把A(﹣1,0),B(5,0)代入抛物线y=ax2+bx﹣5,得
![]() ,解得:
,解得:![]() ,
,
∴y=x2﹣4x﹣5=(x-2)2-9,
∴顶点坐标为D(2,﹣9);
(2)①存在,
设直线BC的函数解析式为y=kx+b(k≠0),
把B(5,0),C(0,﹣5)代入得![]() ,解得:
,解得:![]() ,
,
∴BC解析式为y=x﹣5,
当x=m时,y=m﹣5,
∴P(m,m﹣5),
当x=2时,y=2﹣5=﹣3,
∴E(2.﹣3),
∵PF∥DE∥y轴,
∴点F的横坐标为m,
当x=m时,y=m2﹣4m﹣5,
∴F(m,m2﹣4m﹣5),
∴PF=(m﹣5)﹣(m2﹣4m﹣5)=﹣m2+5m,
∵E(2,﹣3),D(2,﹣9),
∴DE=﹣3﹣(﹣9)=6,
如图,连接DF,
∵PF∥DE,
∴当PF=DE时,四边形PEDF为平行四边形,
即﹣m2+5m=6,
解得m1=3,m2=2(舍去),
当m=3时,y=3﹣5=2,
此时P(3,﹣2),
∴存在点P(3,﹣2)使四边形PEDF为平行四边形;
②由题意,在Rt△BOC中,OB=OC=5,
∴BC=5![]() ,
,
∴C△BOC =10+5![]() ,
,
∵PF∥DE∥y轴,
∴∠FPE=∠DEC=∠OCB,
∵FH⊥BC,
∴∠FHP=∠BOC=90°,
∴△PFH∽△BCO,
∴![]() ,
,
即C△PFH=![]() ,
,
∵0<m<5,
∴当m=﹣![]() 时,△PFH周长的最大值为
时,△PFH周长的最大值为![]() .
.

 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案