Question

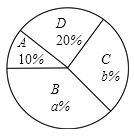
【题目】在“五四青年节”来临之际，某校举办了以“我的青春我做主”为主题的演讲比赛．并从参加比赛的学生中随机抽取部分学生的演讲成绩进行统计（等级记为：优秀，：良好，：一般，：较差），并制作了如下统计图表（部分信息未给出）．

等级	人数
	20
	10

请根据统计图表中的信息解答下列问题：

（1）这次共抽取了______名参加演讲比赛的学生，统汁图中________，_______；

（2）求扇形统计图中演讲成绩等级为“一般”所对应扇形的圆心角的度数；

（3）若该校学生共2000人，如果都参加了演讲比赛，请你估计成绩达到优秀的学生有多少人？

（4）若演讲比赛成绩为等级的学生中恰好有2名女生，其余的学生为男生，从等级的学生中抽取两名同学参加全市演讲比赛，请用列表或画树状图的方法求出“恰好抽中—名男生和一名女生”的概率．

Answer 1

【答案】（1）50，40，30；（2）；（3）200人；（4）

【解析】

（1）根据D等级的人数和对应百分比可得抽取的人数，再分别求得等级B的人数所占百分比和等级C的人数所占百分比即可得出a，b的值；

（2）扇形统计图中演讲成绩等级为“一般”的为C类，所对应扇形的圆心角的度数为：

（3）用等级A的人数所占百分比乘以2000即可

（4）用列表法列出所有情况，再根据概率公式即可求得

（1）这次抽取的演讲比赛的学生人数为10÷20%=50(名)

等级B的学生所占百分比为：×100%=40%

∴a=40

等级C的学生所占百分比为110%20%40%=30%

∴b=30

故答案为：50，40，30

（2）扇形统计图中演讲成绩等级为“一般”的为C类，所对应扇形的圆心角的度数为：

故答案为：

（3）估计成绩达到优秀的人数为：2000×10%=200(人)

故答案为：200人

（4）A等级的学生共有50×10%=5(名)，其中有2名女生，那么男生有3名，
列表分析如下：

	女1	女2	男1	男2	男3
女1		女1女2	女1男1	女1男2	女1男3
女2	女2女1		女2男1	女2男2	女2男3
男1	男1女1	男1女2		男1男2	男1男3
男2	男2女1	男2女2	男2男1		男2男3
男3	男3女1	男3女2	男3男1	男3男2

由上表可知，一共有20种等可能的结果，其中抽中一名男生和一名女生的结果有12种，

则P(抽中一名男生和一名女生)=

故答案为：