题目内容
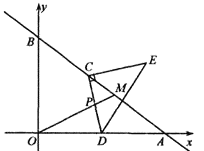
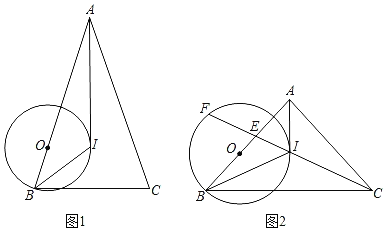
【题目】如图,扇形![]() ,且
,且![]() ,
,![]() ,
,![]() 为弧
为弧![]() 上任意一点,过
上任意一点,过![]() 点作
点作![]() 于点
于点![]() ,设
,设![]() 的内心为
的内心为![]() ,连接
,连接![]() 、
、![]() .当点
.当点![]() 从点
从点![]() 运动到点
运动到点![]() 时,内心
时,内心![]() 所经过的路径长为________.
所经过的路径长为________.
【答案】![]() .
.
【解析】
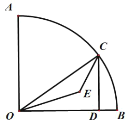
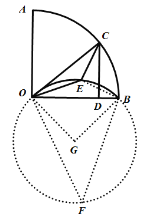
根据E为直角三角形OCD的内心,求出∠OEC=135°,连接BE,证明△OCE≌△OBE,得到∠OEB=135°,得到点E路径为以OB为弦,所对圆心角为135°的圆弧,构造⊙G,求出∠G=90°,![]() ,根据弧长公式计算即可.
,根据弧长公式计算即可.
解:如图,∵![]() ,
,
∴∠COD+∠OCD=90°,
∵E为直角三角形OCD的内心,
∴OE、CE分别平分∠COD、∠OCD,
∴∠OEC=![]() ,
,
连接BE,
∵OE=OE,OC=OC,∠COE=∠BOE
∴△COE≌△BOE
∴∠OEB=∠OEC=135°
∴点E的路径为以OB为弦,所对圆心角为135°的圆弧,
过点O、E、B作圆G,作圆内接四边形OEBF,则∠F=45°,
∴∠G=90°,
∵OG=OB,OB=4,
∴OG=![]() ,
,
∴弧OB长为:![]() .
.
故答案为:![]()

【题目】在“五四青年节”来临之际,某校举办了以“我的青春我做主”为主题的演讲比赛.并从参加比赛的学生中随机抽取部分学生的演讲成绩进行统计(等级记为![]() :优秀,
:优秀,![]() :良好,
:良好,![]() :一般,
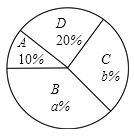
:一般,![]() :较差),并制作了如下统计图表(部分信息未给出).
:较差),并制作了如下统计图表(部分信息未给出).
等级 | 人数 |
|
|
| 20 |
|
|
| 10 |
请根据统计图表中的信息解答下列问题:
(1)这次共抽取了______名参加演讲比赛的学生,统汁图中![]() ________,
________,![]() _______;
_______;
(2)求扇形统计图中演讲成绩等级为“一般”所对应扇形的圆心角的度数;
(3)若该校学生共2000人,如果都参加了演讲比赛,请你估计成绩达到优秀的学生有多少人?
(4)若演讲比赛成绩为![]() 等级的学生中恰好有2名女生,其余的学生为男生,从
等级的学生中恰好有2名女生,其余的学生为男生,从![]() 等级的学生中抽取两名同学参加全市演讲比赛,请用列表或画树状图的方法求出“恰好抽中—名男生和一名女生”的概率.
等级的学生中抽取两名同学参加全市演讲比赛,请用列表或画树状图的方法求出“恰好抽中—名男生和一名女生”的概率.