题目内容
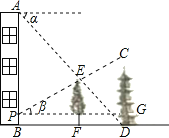
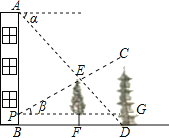
【题目】如图,在一居民楼AB和塔CD之间有一棵树EF,从楼顶A处经过树顶E点恰好看到塔的底部D点,且俯角α为38°.从距离楼底B点2米的P处经过树顶E点恰好看到塔的顶部C点,且仰角β为28°.已知树高EF=8米,求塔CD的高度.(参考数据:sin38°≈0.6,cos38°≈0.8,tan38°≈0.8,sin28°≈0.5,cos28°≈0.9,tan28°≈0.5)
【答案】CD=13(米).
【解析】
根据题意求出∠EDF=38°,通过解直角△EFD求得FD,在Rt△PEH中,利用特殊角的三角函数值分别求出BF,即可求得PG,在Rt△PCG中,继而可求出CG的长度.
解:由题意知,∠EDF=α=38°,
∴FD=![]() =10(米).EH=8﹣2=6(米)
=10(米).EH=8﹣2=6(米)
在Rt△PEH中,∵![]() .
.
∴![]() .
.
∴BF=12(米)
PG=BD=BF+FD=12+10=22(米).
在直角△PCG中,∵![]() .
.
∴CG=PGtanβ≈22×0.5=11(米).
∴CD=11+2=13(米).

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案【题目】在“五四青年节”来临之际,某校举办了以“我的青春我做主”为主题的演讲比赛.并从参加比赛的学生中随机抽取部分学生的演讲成绩进行统计(等级记为![]() :优秀,
:优秀,![]() :良好,
:良好,![]() :一般,
:一般,![]() :较差),并制作了如下统计图表(部分信息未给出).
:较差),并制作了如下统计图表(部分信息未给出).
等级 | 人数 |
|
|
| 20 |
|
|
| 10 |
请根据统计图表中的信息解答下列问题:
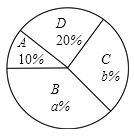
(1)这次共抽取了______名参加演讲比赛的学生,统汁图中![]() ________,
________,![]() _______;
_______;
(2)求扇形统计图中演讲成绩等级为“一般”所对应扇形的圆心角的度数;
(3)若该校学生共2000人,如果都参加了演讲比赛,请你估计成绩达到优秀的学生有多少人?
(4)若演讲比赛成绩为![]() 等级的学生中恰好有2名女生,其余的学生为男生,从
等级的学生中恰好有2名女生,其余的学生为男生,从![]() 等级的学生中抽取两名同学参加全市演讲比赛,请用列表或画树状图的方法求出“恰好抽中—名男生和一名女生”的概率.
等级的学生中抽取两名同学参加全市演讲比赛,请用列表或画树状图的方法求出“恰好抽中—名男生和一名女生”的概率.