Question

【题目】如图，一次函数与反比例函数的图像交于A（1，12）和B（6，2）两点．点P是线段AB上一动点（不与点A和B重合），过P点分别作x、y轴的垂线PC、PD交反比例函数图像于点M、N，则四边形PMON面积的最大值是 ．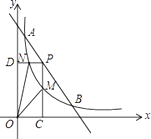

Answer 1

【答案】
【解析】解：设反比例函数解析式为y= ，一次函数解析式为y=kx+b， 由已知得：12= 和 ，
解得：m=12和 ．
∴一次函数解析式为y=﹣2x+14，反比例函数解析式为y= ．
∵点P在线段AB上，
∴设点P的坐标为（n，﹣2n+14）（1＜n＜6）．
令x=n，则y= ；
令y=﹣2n+14，则 =﹣2n+14，解得：x= ．
∴点M（n， ），点N（ ，﹣2n+14）．
S四边形PMON=S矩形OCPD﹣S△ODN﹣S△OCM=n（﹣2n+14）﹣ n ﹣ （﹣2n+14）=﹣2n2+14n﹣12=﹣2 + ．
∴当n= 时，四边形PMON面积最大，最大面积为 ．
故答案为： ．
由点A、B的坐标利用待定系数法即可求出一次函数与反比例函数的解析式，设出点P的坐标为（n，﹣2n+14）（1＜n＜6）．由反比例的函数解析式表示出来M、N点的坐标，分割矩形OCPD，结合矩形和三角形的面积公式即可得出结论．