Question

【题目】如图1，以△ABC的边AB、AC为边分别向外作等腰直角△ABD和等腰直角△ACE，连接CD、BE、DE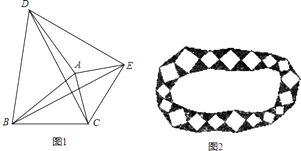
（1）证明：△ADC≌△ABE；
（2）试判断△ABC与△ADE面积之间的关系，并说明理由；
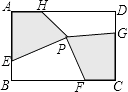
（3）园林小路，曲径通幽，如图2所示，小路由白色的正方形大理石和黑色的三角形大理石铺成，已知中间的所有正方形的面积之和是a平方米，内圈的所有三角形的面积之和是b平方米，这条小路一共占地平方米．（不用写过程）

Answer 1

【答案】
（1）证明：∵△ABD和△ACE都为等腰直角三角形，

∴AD=AB，AE=AC，∠DAB=∠EAC=90°，

∴∠DAB+∠BAC=∠EAC+∠BAC，即∠DAC=∠BAE，

在△DAC和△BAE中，

，

∴△DAC≌△BAE（SAS）

（2）△ABC与△ADE面积相等．

证明：∵△ABD和△ACE都是等腰直角三角形，

∴∠BAD=∠CAE=90°，AB=AD，AC=AE，

∵∠BAD+∠CAD+∠BAC+∠DAE=360°，

∴∠BAC+∠DAE=180°，

∵∠DAE+∠EAN=180°，

∴∠BAC=∠EAN，

在△ACM和△AEN中，

，

∴△ACM≌△AEN（AAS），

∴CM=EN，

∵S△ABC= ABCM，S△ADE= ADEN，

∴S△ABC=S△ADE

（3）（a+2b）
【解析】（3）解：由（2）知外圈的所有三角形的面积之和等于内圈的所有三角形的面积之和． ∴这条小路的面积为（a+2b）平方米．
所以答案是：（a+2b）．

【考点精析】通过灵活运用等腰直角三角形，掌握等腰直角三角形是两条直角边相等的直角三角形；等腰直角三角形的两个底角相等且等于45°即可以解答此题．