题目内容
【题目】如图，直线y=﹣ 
x+2 与x轴，y轴分别交于点A，点B，两动点D，E分别从点A，点B同时出发向点O运动（运动到点O停止），运动速度分别是1个单位长度/秒和 个单位长度/秒，设运动时间为t秒，以点A为顶点的抛物线经过点E，过点E作x轴的平行线，与抛物线的另一个交点为点G，与AB相交于点F．
（1）求点A，点B的坐标；
（2）用含t的代数式分别表示EF和AF的长；
（3）当四边形ADEF为菱形时，试判断△AFG与△AGB是否相似，并说明理由．
（4）是否存在t的值，使△AGF为直角三角形？若存在，求出这时抛物线的解析式；若不存在，请说明理由．
【答案】
（1）解：在直线y=﹣ 
x+2 中，
令y=0可得0=﹣ x+2 ，解得x=2，
令x=0可得y=2 ，
∴A为（2，0），B为（0，2 ）；
（2）解：由（1）可知OA=2，OB=2 ，
∴tan∠ABO= 
= 
，
∴∠ABO=30°，
∵运动时间为t秒，
∴BE= t，
∵EF∥x轴，
∴在Rt△BEF中，EF=BEtan∠ABO= BE=t，BF=2EF=2t，
在Rt△ABO中，OA=2，OB=2 ，
∴AB=4，
∴AF=4﹣2t；
（3）解：相似．理由如下：
当四边形ADEF为菱形时，则有EF=AF，
即t=4﹣2t，解得t= 
，
∴AF=4﹣2t=4﹣ 
= ，OE=OB﹣BE=2 ﹣ × = 
，
如图，过G作GH⊥x轴，交x轴于点H，
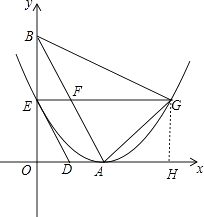
则四边形OEGH为矩形，
∴GH=OE= ，
又EG∥x轴，抛物线的顶点为A，
∴OA=AH=2，
在Rt△AGH中，由勾股定理可得AG2=GH2+AH2=（ ）2+22= 
，
又AFAB= ×4= ，
∴AFAB=AG2，即 
= 
，且∠FAG=∠GAB，
∴△AFG∽△AGB；
（4）解：存在，
∵EG∥x轴，
∴∠GFA=∠BAO=60°，
又G点不能在抛物线的对称轴上，
∴∠FGA≠90°，
∴当△AGF为直角三角形时，则有∠FAG=90°，
又∠FGA=30°，
∴FG=2AF，
∵EF=t，EG=4，
∴FG=4﹣t，且AF=4﹣2t，
∴4﹣t=2（4﹣2t），
解得t= ，
即当t的值为 秒时，△AGF为直角三角形，此时OE=OB﹣BE=2 ﹣ t=2 ﹣ × = ，
∴E点坐标为（0， ），
∵抛物线的顶点为A，
∴可设抛物线解析式为y=a（x﹣2）2，
把E点坐标代入可得 =4a，解得a= 
，
∴抛物线解析式为y= （x﹣2）2，
即y= x2﹣ x+ ．
【解析】（1）在直线y=﹣ 3 x+23 中，令y=0，x=0，得到A为（2，0），B为（0，2 ）；（2）由（1）可知OA=2，OB=2 3 ，得到tan∠ABO
，由∠ABO=30°，由运动时间为t秒，得到BE= t，EF∥x轴，所以在Rt△BEF中，EF=BEtan∠ABO=t，BF=2EF=2t，在Rt△ABO中，OA=2，OB=2 ，所以AB=4，AF=4﹣2t；（3）当四边形ADEF为菱形时，则有EF=AF，即t=4﹣2t，得到AF=4﹣2t= ，OE=OB﹣BE= ，由图知四边形OEGH为矩形，得到GH=OE，又EG∥x轴，抛物线的顶点为A，得到OA=AH=2，在Rt△AGH中，由勾股定理可得AG2=GH2+AH2 ，得到AFAB=AG2，且∠FAG=∠GAB，得到△AFG∽△AGB；（4）由EG∥x轴，得到∠GFA=∠BAO=60°，又G点不能在抛物线的对称轴上，所以∠FGA≠90°，当△AGF为直角三角形时，则有∠FAG=90°，又∠FGA=30°，得到FG=2AF，由EF=t，EG=4，得到FG=4﹣t，且AF=4﹣2t，即当t的值为 秒时，△AGF为直角三角形，此时OE=OB﹣BE，即E点坐标为（0， ），由抛物线的顶点为A，得到可设抛物线解析式为y=a（x﹣2）2，把E点坐标代入可得 =4a，解得a= ，所以抛物线解析式为y= （x﹣2）2，即y= x2﹣ x+ ．
【考点精析】利用相似三角形的判定对题目进行判断即可得到答案，需要熟知相似三角形的判定方法:两角对应相等，两三角形相似（ASA）；直角三角形被斜边上的高分成的两个直角三角形和原三角形相似； 两边对应成比例且夹角相等，两三角形相似（SAS）；三边对应成比例，两三角形相似（SSS）．
