题目内容
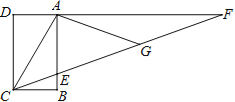
【题目】如图，矩形ABCD中，AD=
，F是DA延长线上一点，G是CF上一点，且∠ACG=∠AGC，∠GAF=∠F=20°，则AB= ．
【答案】
.
【解析】试题分析：根据三角形的一个外角等于与它不相邻的两个内角的和可得∠AGC=∠GAF+∠F=40°，再根据等腰三角形的性质求出∠CAG，然后求出∠CAF=120°，再根据∠BAC=∠CAF-∠BAF求出∠BAC=30°，再根据直角三角形30°角所对的直角边等于斜边的一半可得AC=2BC=2AD，然后利用勾股定理列式计算即可得解．
试题解析：由三角形的外角性质得，∠AGC=∠GAF+∠F=20°+20°=40°，
∵∠ACG=∠AGC，
∴∠CAG=180°-∠ACG-∠AGC=180°-2×40°=100°，
∴∠CAF=∠CAG+∠GAF=100°+20°=120°，
∴∠BAC=∠CAF-∠BAF=30°，
在Rt△ABC中，AC=2BC=2AD=2
，
由勾股定理，AB=
．
练习册系列答案
相关题目
