题目内容
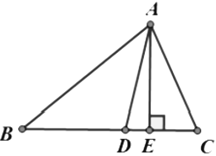
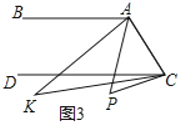
【题目】如图,抛物线y=ax2+bx﹣4与x轴交于A(4,0)、B(﹣2,0)两点,与y轴交于点C,点P是线段AB上一动点(端点除外),过点P作PD∥AC,交BC于点D,连接CP.
(1)求该抛物线的解析式;
(2)当动点P运动到何处时,BP2=BDBC;
(3)当△PCD的面积最大时,求点P的坐标.
【答案】
(1)解:由题意,得 ![]() ,
,
解得  ,
,
∴抛物线的解析式为y= ![]() ﹣x﹣4
﹣x﹣4

(2)解:设点P运动到点(x,0)时,有BP2=BDBC,
令x=0时,则y=﹣4,
∴点C的坐标为(0,﹣4).
∵PD∥AC,
∴△BPD∽△BAC,
∴ ![]() .
.
∵BC= ![]() =
= ![]() =2
=2 ![]() ,
,
AB=6,BP=x﹣(﹣2)=x+2.
∴BD= ![]() =
= ![]() =
= ![]() .
.
∵BP2=BDBC,
∴(x+2)2= ![]() ×2
×2 ![]() ,
,
解得x1= ![]() ,x2=﹣2(﹣2不合题意,舍去),
,x2=﹣2(﹣2不合题意,舍去),
∴点P的坐标是( ![]() ,0),即当点P运动到(
,0),即当点P运动到( ![]() ,0)时,BP2=BDBC;
,0)时,BP2=BDBC;
(3)解:∵△BPD∽△BAC,
∴ ![]() ,
,
∴ ![]() ×
× ![]()
S△PDC=S△PBC﹣S△PBD= ![]() ×(x+2)×4﹣
×(x+2)×4﹣ ![]()
∵ ![]() ,
,
∴当x=1时,S△PDC有最大值为3.
即点P的坐标为(1,0)时,△PDC的面积最大.
【解析】(1)用待定系数法求出抛物线的解析式,把A(4,0)、B(﹣2,0)两点,代入抛物线y=ax2+bx﹣4即可;(2)求出点C的坐标为(0,﹣4),由PD∥AC,得到△BPD∽△BAC,得到比例,由勾股定理得到BC= ![]() ,求出BD的值,由BP2=BDBC,求出点P的坐标是( img src="http://thumb.zyjl.cn/questionBank/Upload/2018/02/24/00/3e4277fa/SYS201802240015451442469337_DA/SYS201802240015451442469337_DA.012.png" width="9" height="32" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" /> ,0),即当点P运动到(
,求出BD的值,由BP2=BDBC,求出点P的坐标是( img src="http://thumb.zyjl.cn/questionBank/Upload/2018/02/24/00/3e4277fa/SYS201802240015451442469337_DA/SYS201802240015451442469337_DA.012.png" width="9" height="32" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" /> ,0),即当点P运动到( ![]() ,0)时,BP2=BDBC;(3)由△BPD∽△BAC,得到
,0)时,BP2=BDBC;(3)由△BPD∽△BAC,得到 ![]() ,
, ![]()
![]() ;S△PDC=S△PBC﹣S△PBD ,得到当x=1时,S△PDC有最大值为3,即点P的坐标为(1,0)时,△PDC的面积最大.
;S△PDC=S△PBC﹣S△PBD ,得到当x=1时,S△PDC有最大值为3,即点P的坐标为(1,0)时,△PDC的面积最大.

【题目】某校对“学生在学校拿手机影响学习的情况”进行了调查,随机调查了部分学生,对此问题的看法分为三种情况:没有影响、影响不大、影响很大,并将调查结果绘制成如下不完整的统计表和扇形统计图,根据统计图表提供的信息,解答下列问题:
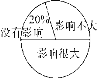
人数统计表如下:
看法 | 没有影响 | 影响不大 | 影响很大 |
学生人数(人) | 20 | 30 | a |
(1)统计表中的a= ;
(2)请根据表中的数据,谈谈你的看法(不少于2条)
【题目】有一等腰直角三角形纸片,以它的对称轴为折痕,将三角形对折,得到的三角形还是等腰直角三角形(如图).依照上述方法将原等腰直角三角形折叠四次,所得小等腰直角三角形的周长是原等腰直角三角形周长的倍.
【题目】某商店甲、乙两种商品三天销售情况的账目记录如下表:
日期 | 卖出甲商品的数量(个) | 卖出乙商品的数量(个) | 收入(元) |
第一天 | 39 | 21 | 321 |
第二天 | 26 | 14 | 204 |
第三天 | 39 | 25 | 345 |
(1)财务主管在核查时发现:第一天的账目正确,但其他两天的账目有一天有误,请你判断第几天的账目有误,并说明理由;
(2)求甲、乙两种商品的单价.