题目内容
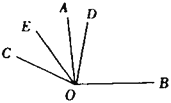
【题目】如图所示,在平面直角坐标系中,过点A(﹣ ![]() ,0)的两条直线分别交y轴于B,C两点,且B,C两点的纵坐标分别是一元二次方程x2﹣2x﹣3=0的两个根.
,0)的两条直线分别交y轴于B,C两点,且B,C两点的纵坐标分别是一元二次方程x2﹣2x﹣3=0的两个根.
(1)求线段BC的长度;
(2)试问:直线AC与直线AB是否垂直?请说明理由;
(3)若点D在直线AC上,且DB=DC,求点D的坐标.
【答案】
(1)解:∵x2﹣2x﹣3=0,
∴x=3或x=﹣1,
∴B(0,3),C(0,﹣1),
∴BC=4;
(2)解:垂直,理由如下:
∵A(﹣ ![]() ,0),B(0,3),C(0,﹣1),
,0),B(0,3),C(0,﹣1),
∴OA= ![]() ,OB=3,OC=1,
,OB=3,OC=1,
∴OA2=OBOC,
∵∠AOC=∠BOA=90°,
∴△AOC∽△BOA,
∴∠CAO=∠ABO,
∴∠CAO+∠BAO=∠ABO+∠BAO=90°,
∴∠BAC=90°,
∴AC⊥AB;
(3)解:设直线AC的解析式为y=kx+b,
把A(﹣ ![]() ,0)和C(0,﹣1)代入y=kx+b,
,0)和C(0,﹣1)代入y=kx+b,
∴ ![]() ,解得
,解得 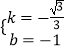 ,
,
∴直线AC的解析式为y=﹣ ![]() x﹣1,
x﹣1,
∵DB=DC,
∴点D在线段BC的垂直平分线上,
∴D的纵坐标为1,
∴把y=1代入y=﹣ ![]() x﹣1,
x﹣1,
∴x=﹣2 ![]() ,
,
∴D的坐标为(﹣2 ![]() ,1).
,1).
【解析】(1)解方程x2﹣2x﹣3=0求得x的值,从而可得到BC的长;
(2)利用A、B、C的坐标,求得OA、OB、OC的长,可证明△AOC∽△BOA,从而求得∠BAC=90°,得证;
(3)由A、C坐标,利用待定系数法求得直线AC的解析式,结合条件可得D在线段BC的垂直平分线上,可求得D点的坐标.

【题目】某校对“学生在学校拿手机影响学习的情况”进行了调查,随机调查了部分学生,对此问题的看法分为三种情况:没有影响、影响不大、影响很大,并将调查结果绘制成如下不完整的统计表和扇形统计图,根据统计图表提供的信息,解答下列问题:
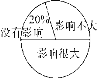
人数统计表如下:
看法 | 没有影响 | 影响不大 | 影响很大 |
学生人数(人) | 20 | 30 | a |
(1)统计表中的a= ;
(2)请根据表中的数据,谈谈你的看法(不少于2条)