ЬтФПФкШн
ЁОЬтФПЁПШчЙћСНИіНЧжЎВюЕФОјЖджЕЕШгк60ЁуЃЌдђГЦетСНИіНЧЛЅЮЊЁАЛЅгХНЧЁБЃЌ(БОЬтжаЫљгаНЧЖМЪЧжИДѓгк0ЁуЧваЁгк180ЁуЕФНЧ)ЃЎ
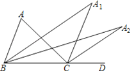
(1)ШєЁЯ1КЭЁЯ2ЛЅЮЊЁАЛЅгХНЧЁБЃЌЕБЁЯ1=90ЁуЪБЃЌдђЁЯ2=_____ЁуЃЛ
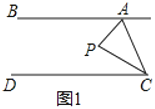
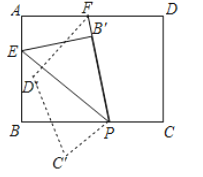
(2)ШчЭМ1ЃЌНЋвЛГЄЗНаЮжНЦЌбизХEPЖдел(ЕуPдкЯпЖЮBCЩЯЃЌЕуEдкЯпЖЮABЩЯ)ЪЙЕуBТфдкЕуШєгыЛЅЮЊЁАЛЅгХНЧЁБЃЌЧѓЁЯBPEЕФЖШЪ§ЃЛ
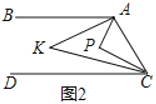
(3)дйНЋжНЦЌбизХPFЖдел(ЕуFдкЯпЖЮCDЛђADЩЯ)ЪЙЕуCТфдкCЁфЃК
ЂйШчЭМ2ЃЌШєЕуEЁЂCЁфЁЂPдкЭЌвЛжБЯпЩЯЃЌЧв![]() гы
гы![]() ЛЅЮЊЁАЛЅгХНЧЁБЃЌЧѓЁЯEPFЕФЖШЪ§(ЖделЪБЃЌЯпЖЮТфдкЁЯEPFФкВП)ЃЛ
ЛЅЮЊЁАЛЅгХНЧЁБЃЌЧѓЁЯEPFЕФЖШЪ§(ЖделЪБЃЌЯпЖЮТфдкЁЯEPFФкВП)ЃЛ
ЂкШєЁЯBЁфPCЁфгыЁЯEPFЛЅЮЊЁАЛЅгХНЧЁБЃЌдђЁЯBPEЧѓЁЯCPFгІТњзуЪВУДбљЕФЪ§СПЙиЯЕ(жБНгаДГіНсЙћМДПЩ)ЃЎ

ЁОД№АИЁПЃЈ1ЃЉ30ЁуЛђ150ЃЛЃЈ2ЃЉ40ЁуЛђ80ЁуЃЛЃЈ3ЃЉЂйЁЯEPF=80ЁуЃЌЂкЁЯEPF=40ЁуЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉАДееЁАЛЅгХНЧЕФЖЈвхЃЌЧѓГіЁЯ2МДПЩЃЛ
ЃЈ2ЃЉИљОнЁЯEPB'+ЁЯEPB'+ЁЯEPB'+60Ёу=180ЁуНтД№МДПЩЃЛ
ЃЈ3ЃЉЂйгЩЁЯBPE+ЁЯEPB'+ЁЯB'PF+ЁЯFPC=180ЁуНтД№МДПЩЃЛ
ЂкЁЯB'PC'=ЁЯFPCЃЌЁЯEPB=ЁЯEPFЃЌЁЯEPB+ЁЯEPF+ЁЯFPC=180ЁуНтД№МДПЩЃЎ
НтЃКЃЈ1ЃЉЁпЁЯ1КЭЁЯ2ЛЅЮЊЁАЛЅгХНЧ
Ёр|ЁЯ1-ЁЯ2|=60Ёу
ЁпЁЯ1ЃН90Ёу
Ёр90Ёу-ЁЯ2=60ЁуЛђ90Ёу-ЁЯ2=-60Ёу
НтЕУЃКЁЯ2=30ЁуЛђ150Ёу
ЙЪД№АИЮЊЃК30ЁуЛђ150ЃЎ
ЃЈ2ЃЉЁпЁЯEPB'гыЁЯB'PCЛЅЮЊЁАЛЅгХНЧЁБ
ЕБЁЯEPB'<ЁЯB'PCЪБЃЌЁЯB'PC-ЁЯEPB'=60Ёу
ЁрЁЯB'PC=ЁЯEPB'+60Ёу
ЁпЁїBEPЗелЕУЁїB'EP
ЁрЁЯEPB=ЁЯEPB'
ЁпЁЯEPB+ЁЯEPB'+ЁЯB'PC=180Ёу
ЁрЁЯEPB'+ЁЯEPB'+ЁЯEPB'+60Ёу=180
НтЕУЃКЁЯEPB'=40Ёу
ЕБЁЯEPB'>ЁЯB'PCЪБЃЌЁЯB'PC-ЁЯEPB'=60ЁуЃЌПЩЕУЁЯEPB'=80Ёу
ЙЪЁЯEPB'ЕФжЕЮЊ40ЁуЛђ80ЁуЃЛ
ЃЈ3ЃЉЂйгЩЬтвтЕУЃКЕуEЁЂCЁЂPдкЭЌвЛжБЯпЩЯЃЌ
ЁпЁЯB'PC'гыЁЯEPFЛЅЮЊЁАЛЅгХНЧ
ЁрЁЯBPC<ЁЯEPFЃЌЁЯEPF-ЁЯB'PC=60Ёу=ЁЯB'PF
ЁпЁЯBPE=ЁЯB'PC=ЁЯEPF-60ЁуЃЌЁЯFPC=ЁЯEPF
ЁрЁЯBPE+ЁЯEPB'+ЁЯB'PF+ЁЯFPC=180Ёу
ЁрЁЯEPF-60Ёу+ЁЯEPF+ЁЯEPF=180ЁуЃЌЕУЁЯEPF=80ЁуЃЛ
ЂкгЩЬтвтЕУЃКЕуEЁЂCЁЂPдкЭЌвЛжБЯпЩЯЃЌ
ЁпЁЯB'PC'гыЁЯEPFЛЅЮЊЁАЛЅгХНЧ
ЁрЁЯB'P'C-ЁЯEPF=60ЁуЃЌЕУЁЯB'P'C=60Ёу+ЁЯEPF
ЁпЁЯB'PC'=ЁЯFPCЃЌЁЯEPB=ЁЯEPFЃЌЁЯEPB+ЁЯEPF+ЁЯFPC=180Ёу
Ёр2ЁЯEPF+60Ёу+ЁЯEPF=180ЁуЃЌНтЕУЁЯEPF=40ЁуЃЎ
ЙЪЁЯEPFЕФЖШЪ§ЮЊ40ЁуЃЎ

 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИЁОЬтФПЁПФГаЃЖдЁАбЇЩњдкбЇаЃФУЪжЛњгАЯьбЇЯАЕФЧщПіЁБНјааСЫЕїВщЃЌЫцЛњЕїВщСЫВПЗжбЇЩњЃЌЖдДЫЮЪЬтЕФПДЗЈЗжЮЊШ§жжЧщПіЃКУЛгагАЯьЁЂгАЯьВЛДѓЁЂгАЯьКмДѓЃЌВЂНЋЕїВщНсЙћЛцжЦГЩШчЯТВЛЭъећЕФЭГМЦБэКЭЩШаЮЭГМЦЭМЃЌИљОнЭГМЦЭМБэЬсЙЉЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ШЫЪ§ЭГМЦБэШчЯТЃК
ПДЗЈ | УЛгагАЯь | гАЯьВЛДѓ | гАЯьКмДѓ |
бЇЩњШЫЪ§(ШЫ) | 20 | 30 | a |
ЃЈ1ЃЉЭГМЦБэжаЕФaЃНЁЁЁЁЁЁЁЁЃЛ
ЃЈ2ЃЉЧыИљОнБэжаЕФЪ§ОнЃЌЬИЬИФуЕФПДЗЈЃЈВЛЩйгк2ЬѕЃЉ