题目内容
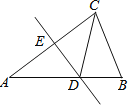
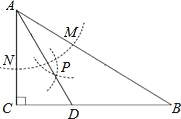
【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧交AB于M、AC于N,再分别以M、N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于D,下列四个结论:
MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于D,下列四个结论:
①AD是∠BAC的平分线;
②∠ADC=60°;
③点D在AB的中垂线上;
④S△ACD:S△ACB=1:3.
其中正确的有( )
A. 只有①②③ B. 只有①②④ C. 只有①③④ D. ①②③④
【答案】D
【解析】
①根据作图过程可判定AD是∠BAC的角平分线;②利用角平分线的定义可推知∠CAD=30°,则由直角三角形的性质来求∠ADC的度数;③利用等角对等边可以证得△ADB是等腰三角形,由等腰三角形的“三合一”性质可以证明点D在AB的中垂线上;④利用30°角所对的直角边是斜边的一半,三角形的面积计算公式来求两个三角形面积之比.
①根据作图过程可知AD是∠BAC的角平分线,①正确;②如图,在△ABC中,∠C=90°,∠B=30°,∴∠CAB=60°,又∵AD是∠BAC的平分线,∴∠1=∠2=![]() ∠CAB=30°,∴∠3=90°-∠2=60°,即∠ADC=60°,②正确;③∵∠1=∠B=30°,∴AD=BD,∴点D在AB的中垂线上,③正确;④如图,∵在直角△ACD中,∠2=30°,∴CD=
∠CAB=30°,∴∠3=90°-∠2=60°,即∠ADC=60°,②正确;③∵∠1=∠B=30°,∴AD=BD,∴点D在AB的中垂线上,③正确;④如图,∵在直角△ACD中,∠2=30°,∴CD=![]() AD,∴BC=CD+BD=
AD,∴BC=CD+BD=![]() AD+AD=
AD+AD=![]() AD,S△DAC=
AD,S△DAC=![]() ACCD=
ACCD=![]() ACAD.∴S△ABC=
ACAD.∴S△ABC=![]() ACBC=
ACBC=![]() AC
AC![]() AD=
AD=![]() ACAD,∴S△DAC:S△ABC=
ACAD,∴S△DAC:S△ABC=![]() ACAD:
ACAD:![]() ACAD=1:3,④正确.故选D.
ACAD=1:3,④正确.故选D.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目